Все статьи Взрыв на цветочной фабрике
Мы рассмотрим, как с помощью теории вероятности симулировать физическую систему из множества простых частиц
В прошлых уроках мы применяли линейную алгебру и тригонометрию. Теперь пришло время теории вероятностей: именно она позволяет симулировать связанную физическими законами систему из множества простых частиц, таких как дым, огонь, молния, дождь, брызги воды, пар или облака.
Используемый в примере способ будет неэффективен в плане производительности — в будущем мы глубже изучим OpenGL и повысим производительность системы частиц.
Случайность в C и C++11
В дискретном мире компьютеров нет абсолютно случайных чисел. Современные операционные системы позволяет получить почти случайные числа — настолько хорошие, что их даже можно использовать в криптографии. Но скорость получения криптографически случайных чисел низкая, а скорость регенерации пула этих чисел конечная.
Играм не нужна криптографически надёжная случайность. Традиционный подход — получать случайное число на основе времени запуска подпрограммы, и считать это число семенем (англ. seed), позволяющим вырастить целую последовательность чисел, зависимость которых друг от друга трудно проследить снаружи. Такие последовательности называются псевдо-случайными (англ. pseudo-random).
В C++14 есть два стандартных способа генерации псевдослучайных чисел:
- функции
rand()иsrand, часть стандарта C89, дают доступ к глобальной для программы последовательности случайных чисел - заголовок
<random>, часть стандарта C++11, даёт классы для создания множества независимых последовательностей и множества семян для них, также он даёт готовые средства для деформирования случайности
Случайный интервал чисел
Допустим, мы хотим изменять число лепестков цветка — с линейным распределением случайности. Мы также хотим изменять время жизни цветков от появления до исчезновения, и тут есть нюанс: мы хотим, чтобы большинство цветков имело среднее время жизни, а на краях допустимого интервала жизни оказывались лишь единицы. Этого можно добиться с помощью нормального распределения случайных чисел:
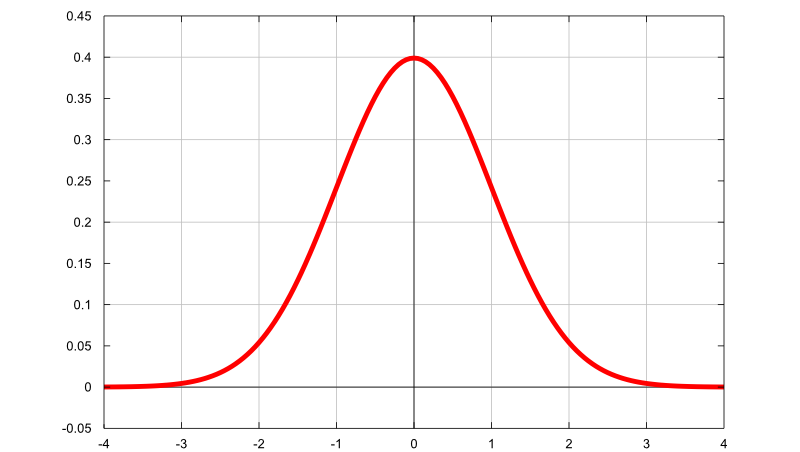
Другой вопрос — как хранить допустимый интервал [minValue, maxValue], представляющий границы случайной последовательности?
- использовать
glm::vec2не стоит, потому что неочевидно, что означаютxиy - для
std::pair<float, float>это более наглядно, но придётся писать отдельные функции и хранить отдельно данные для реализации самой последовательности в этих границах
Третий вопрос — как хранить информацию о самой последовательности, и куда поместить метод для получения нового числа? Можно создать свой шаблонный класс CRandomSequence<T>, и реализовать в нём разные распределения (линейное и нормальное). В конечном счёте вы получите… аналог того, что уже есть в STL.
STL предоставляет готовые классы std::uniform_int_distribution<T>, std::uniform_real_distribution<T> и std::normal_distribution<T>, которые решают сразу три задачи: задают случайное распределение, хранят границы диапазона случайных чисел и позволяют получить новое случайное число на основе предыдущего, которое сохраняется внутри распределения.
Применение случайных интервалов
Случайные распределения STL содержат все нужные данные и методы, но не имеют одного: источника исходных случайных чисел неограниченного диапазона. Для этой цели в STL служат два отдельных класса: std::random_device, дающий новое истинно случайное семя, и std::mt19937, позволяющий из семени получить псевдослучайную последовательность неограниченного диапазона. Распределение является функтором, который при вызове принимает ссылку на источник случайности — либо на сам std::random_device, либо на перемешиватель std::mt19937. Поскольку перемешиватель работает быстрее, следует использовать именно его при вызове функтора.
Сайт cppreference.com предлагает следующий способ:
#include <iostream>
#include <string>
#include <random>
int main()
{
// Запрашивает почти случайное число через API ОС.
std::random_device rd;
// Движок "перемешивания", дающий из одного семени rd() целую цепочку
std::mt19937 engine(rd());
// линейное распределение целых чисел на интервале [1..6]
std::uniform_int_distribution<int> uniform_dist(1, 6);
int mean = uniform_dist(engine);
std::cout << "Randomly-chosen mean: " << mean << '\n';
}
Ограничиваем нормальное распределение
Особенность нормального распределения в том, что оно не имеет границ — значения могут быть любым числам диапазона float, но вероятность появления чисел за пределами определённого интервала очень низкая. Поэтому параметры конструктора normal_distribution<T> принимают отнюдь не минимальное и максимальное значение, а математическое ожидание и среднеквадратическое отклонение. Если мы попробуем генерировать временные интервалы распределением normal_distribution(min, max), мы иногда будем получать отрицательные интервалы времени.
В ответе на stackoverflow.com есть отличное объяснение свойств нормального распределения и способа уместить его в определённый диапазон float. Именно так мы и сделаем:
// Создано на основе http://stackoverflow.com/questions/28618900
class CClampedNormalDistribution
{
std::normal_distribution<float> m_distribution;
float m_min = 0.f;
float m_max = 0.f;
public:
// m_distribution требует два параметра:
// `mean`, т.е. медианное значение и одновременно мат. ожидание
// `stddev`, т.е. стандартное отклонение (дисперсию)
// мы выводим эти параметры из min/max.
void param(float min, float max)
{
using param_type = std::normal_distribution<float>::param_type;
const float mean = (min + max) / 2.f;
const float stddev = (max - min) / 6.f;
m_distribution.param(param_type(mean, stddev));
m_min = min;
m_max = max;
}
// Нормальное распределение выдаёт значения на всём диапазоне float
// Но мы режем значения, выпадающие из диапазона [min, max]
// Статистически, будет выброшено около 0.3% значений.
float operator ()(std::mt19937 &random) {
while (true) {
float number = m_distribution(random);
if (number >= m_min && number <= m_max)
return number;
}
}
};
Цветок-частица
Добавим класс CFlowerParticle, который расширяет CMovableFlower новыми свойствами. Нам нужны два новых свойства: двумерный вектор скорости перемещения (англ. velocity) и оставшееся время жизни частицы, после истечения которого частица просто исчезает.
class CFlowerParticle : public CMovableFlower
{
public:
// @param dt - разница во времени с предыдущим вызовом Advance.
// @param acceleration - ускорение, действующее на частицу.
void Advance(float dt, const glm::vec2 &acceleration);
bool IsAlive()const;
glm::vec2 GetVelocity() const;
void SetVelocity(const glm::vec2 &GetVelocity);
void SetLifetime(float lifetime);
private:
glm::vec2 m_velocity;
float m_lifetime = 0;
};
Вместо getter-метода GetLifetime был добавлен более удобный метод IsAlive, проверяющий оставшееся время жизни:
bool CFlowerParticle::IsAlive() const
{
const float epsilon = std::numeric_limits<float>::epsilon();
return m_lifetime > epsilon;
}
Метод Advance принимает прошедший интервал времени и ускорение. В данный момент ускорение всегда постоянное — его порождает сила гравитации. Это можно изменить в будущем, если добавить вентилятор или другой объект, воздействующий на цветы.
void CFlowerParticle::Advance(float dt, const glm::vec2 &acceleration)
{
m_lifetime -= dt;
m_velocity += dt * acceleration;
SetPosition(dt * m_velocity + GetPosition());
}
Система частиц
Добавим класс, реализующий систему из множества частиц. Система собирает воедино сами частицы, законы симулируемого мира и источник новых частиц. В качестве частиц выступит класс CFlowerParticle, а для генерации новых частиц мы применим класс CParticleEmitter, который будет описан позднее. Пока что утвердим его интерфейс:
class CParticleEmitter
{
public:
CParticleEmitter();
// @param dt - разница во времени с предыдущим вызовом Advance.
void Advance(float dt);
bool IsEmitReady()const;
std::unique_ptr<CFlowerParticle> Emit();
};
Источник частиц продвигается вперёд во времени при вызове метода Advance. При этом он может войти в статус готовности генерации, и тогда IsEmitReady вернёт true. Если в такой ситуации вызвать Emit(), источник частиц сгенерирует частицу. Учтите: за один кадр может возникнуть несколько частиц, если частота их генерации превышает частоту кадров. Поэтому IsEmitReady и Emit следует вызывать в цикле.
Собирающий класс системы частиц относительно прост и выглядит так:
class CParticleSystem
{
public:
CParticleSystem();
~CParticleSystem();
void SetEmitter(std::unique_ptr<CParticleEmitter> && pEmitter);
void SetGravity(const glm::vec2 &gravity);
// @param dt - разница во времени с предыдущим вызовом Advance.
void Advance(float dt);
void Draw();
private:
std::unique_ptr<CParticleEmitter> m_pEmitter;
std::vector<std::unique_ptr<CFlowerParticle>> m_flowers;
glm::vec2 m_gravity;
};
Конструктор, деструктор и методы для установки свойств строятся достаточно просто:
CParticleSystem::CParticleSystem() = default;
CParticleSystem::~CParticleSystem() = default;
void CParticleSystem::SetEmitter(std::unique_ptr<CParticleEmitter> &&pEmitter)
{
m_pEmitter = std::move(pEmitter);
}
void CParticleSystem::SetGravity(const glm::vec2 &gravity)
{
m_gravity = gravity;
}
При вызове Advance нужно сгенерировать новые частицы, затем продвинуть в будущее на время deltaSeconds состояние каждого цветка и в конце удалить отжившие своё цветы. Это можно сделать с помощью цикла while, цикла range-based for и алгоритмов remove_if/erase:
void CParticleSystem::Advance(float dt)
{
// Генерируем новые частицы
m_pEmitter->Advance(dt);
// За 1 кадр может появиться несколько новых частиц.
while (m_pEmitter->IsEmitReady())
{
m_flowers.emplace_back(m_pEmitter->Emit());
}
// Продвигаем время жизни всех цветов.
for (const auto &pFlower : m_flowers)
{
pFlower->Advance(dt, m_gravity);
}
// Удаляем "умершие" цветы.
auto newEnd = std::remove_if(m_flowers.begin(), m_flowers.end(), [](const auto &pFlower) {
return !pFlower->IsAlive();
});
m_flowers.erase(newEnd, m_flowers.end());
}
При рисовании мы должны обойти список живых цветов и нарисовать их
void CParticleSystem::Draw()
{
for (const auto &pFlower : m_flowers)
{
pFlower->Draw();
}
}
Источник частиц
Источник частиц будет испускать частицы с помощью случайных распределений. Также ему нужна позиция, т.е. точка возникновения цветов, а ещё объект std::mt19937, создающий исходную псевдослучайную последовательность, которая затем обрабатывается распределениям. Класс имеет достаточно много свойств, потому что мы хотим настраивать множество параметров генерации частиц.
class CParticleEmitter
{
public:
CParticleEmitter();
// @param dt - разница во времени с предыдущим вызовом Advance.
void Advance(float dt);
bool IsEmitReady()const;
std::unique_ptr<CFlowerParticle> Emit();
void SetPosition(const glm::vec2 &value);
void SetLifetimeRange(float minValue, float maxValue);
void SetRadiusRange(float minValue, float maxValue);
void SetPetalsCountRangle(int minValue, int maxValue);
void SetEmitIntervalRange(float minValue, float maxValue);
void SetSpeedRange(float minValue, float maxValue);
void SetAngleRange(float minValue, float maxValue);
private:
using linear_random_float = std::uniform_real_distribution<float>;
using normal_random_float = CClampedNormalDistribution;
using linear_random_int = std::uniform_int_distribution<int>;
float m_elapsedSeconds = 0;
float m_nextEmitTime = 0;
glm::vec2 m_position;
normal_random_float m_lifetimeRange;
linear_random_float m_radiusRange;
linear_random_int m_petalsCountRange;
normal_random_float m_emitIntervalRange;
normal_random_float m_speedRange;
normal_random_float m_angleRange;
std::mt19937 m_random;
};
Реализация методов-сеттеров примерно одинакова:
void CParticleEmitter::SetPosition(const glm::vec2 &value)
{
m_position = value;
}
void CParticleEmitter::SetLifetimeRange(float minValue, float maxValue)
{
m_lifetimeRange.param(minValue, maxValue);
}
// и так далее
Определение интервала испускания частиц устроено следующим образом: в методе Advance мы прибавляем прошедшее время к m_elapsedSeconds, а затем отнимаем время m_nextEmitTime, пока есть возможность, и каждый раз порождаем частицу. При этом следующее значение m_nextEmitTime определяется случайным распределением.
void CParticleEmitter::Advance(float dt)
{
m_elapsedSeconds += dt;
std::cerr << "m_elapsedSeconds increased, is " << m_elapsedSeconds << std::endl;
}
bool CParticleEmitter::IsEmitReady() const
{
return m_elapsedSeconds > m_nextEmitTime;
}
std::unique_ptr<CFlowerParticle> CParticleEmitter::Emit()
{
// Определяем время появления следующей частицы.
m_elapsedSeconds -= m_nextEmitTime;
m_nextEmitTime = m_emitIntervalRange(m_random);
// Остальной код отвечает за генерацию новой частицы
// Чтобы обеспечить basic exception safety, выделение памяти
// следует разместить в начале метода Emit.
}
Весь метод Emit выглядит так:
std::unique_ptr<CFlowerParticle> CParticleEmitter::Emit()
{
const glm::vec3 LIGHT_YELLOW = { 1.f, 1.f, 0.5f};
const glm::vec3 ORANGE = {1.f, 0.5f, 0.f};
auto pFlower = std::make_unique<CFlowerParticle>();
// Определяем время появления следующей частицы.
m_elapsedSeconds -= m_nextEmitTime;
m_nextEmitTime = m_emitIntervalRange(m_random);
const float speed = m_speedRange(m_random);
const float angle = m_angleRange(m_random);
const glm::vec2 velocity = { speed * sinf(angle), speed * cosf(angle) };
const float maxRadius = m_radiusRange(m_random);
const int petalsCount = m_petalsCountRange(m_random);
pFlower->SetLifetime(m_lifetimeRange(m_random));
pFlower->SetVelocity(velocity);
pFlower->SetCenterColor(LIGHT_YELLOW);
pFlower->SetPetalColor(ORANGE);
pFlower->SetPosition(m_position);
pFlower->SetupShape(0.3f * maxRadius, maxRadius, petalsCount);
return pFlower;
}
Изменения в классе CWindow
В классе CWindow сложным будет только конструктор, остальное стало проще или не изменилось с предыдущей версии. Дело в том, что вся логика перенесена в класс CParticleSystem, и остаётся только настроить её в конструкторе.
класс CWindow
class CWindow : public CAbstractInputControlWindow
{
public:
CWindow();
protected:
// CAbstractWindow interface
void OnUpdateWindow(float deltaSeconds) override;
void OnDrawWindow(const glm::ivec2 &size) override;
private:
void SetupView(const glm::ivec2 &size);
CParticleSystem m_system;
};
методы CWindow
CWindow::CWindow()
{
auto pEmitter = std::make_unique<CParticleEmitter>();
pEmitter->SetPosition({0, 600});
pEmitter->SetAngleRange(glm::radians(110.f), glm::radians(160.f));
pEmitter->SetEmitIntervalRange(0.15f, 0.25f);
pEmitter->SetLifetimeRange(10.f, 20.f);
pEmitter->SetPetalsCountRangle(5, 9);
pEmitter->SetRadiusRange(40.f, 75.f);
pEmitter->SetSpeedRange(200.f, 400.f);
m_system.SetEmitter(std::move(pEmitter));
m_system.SetGravity({0, 98});
SetBackgroundColor(QUIET_GREEN);
}
void CWindow::OnUpdateWindow(float deltaSeconds)
{
m_system.Advance(deltaSeconds);
}
void CWindow::OnDrawWindow(const glm::ivec2 &size)
{
SetupView(size);
m_system.Draw();
}
Явное ограничение FPS
Если запустить созданное приложение, можно заметить, что на некоторых видеокартах скорость системы частиц оказывается крайне низкой. Причина неожиданно проста — просто представьте, что будет, если с момента предыдущего кадра произошло менее одной миллисекунды:
float CChronometer::GrabDeltaTime()
{
auto newTime = system_clock::now();
auto timePassed = duration_cast<milliseconds>(newTime - m_lastTime);
m_lastTime = newTime;
return 0.001f * float(timePassed.count());
};
Из кода метода CChronometer::GrabDeltaTime понятно, что при интервале менее чем в одну миллисекунду deltaTime будет нулевым, и продвижение всей системы частиц вперёд во времени будет также нулевым.
Исправить проблему в рамках метода “GrabDeltaTime” затрудительно, потому что системные часы, скрытые за классом system_clock, имеют ограничения по точности, и малые интервалы времени измеряются неточно. Поэтому вместо более точного расчёта промежутков времени мы просто установим минимальный промежуток между двумя кадрами, равный 1second / 60.0 = 16ms, что обеспечит нам около 60 кадров в секунду. Для реализации этой возможности добавим метод CChronometer::WaitNextFrameTime(const milliseconds &framePeriod), который на основе момента времени предыдущего кадра и переданного снаружи параметра “framePeriod” вычисляет момент начала следующего кадра и дожидается его:
#include <thread> // для функции std::this_thread::sleep_until
void CChronometer::WaitNextFrameTime(const milliseconds &framePeriod)
{
system_clock::time_point nextFrameTime = m_lastTime + framePeriod;
std::this_thread::sleep_until(nextFrameTime);
}
Теперь можно исправить метод CAbstractWindow::DoGameLoop(), чтобы после вызова SwapBuffers() ожидать времени, подходящего для рисования следующего кадра:
void CAbstractWindow::DoGameLoop()
{
const std::chrono::milliseconds FRAME_PERIOD(16);
SDL_Event event;
CChronometer chronometer;
while (true)
{
while (SDL_PollEvent(&event) != 0)
{
if (!m_pImpl->ConsumeEvent(event))
{
OnWindowEvent(event);
}
}
if (m_pImpl->IsTerminated())
{
break;
}
// Очистка буфера кадра, обновление и рисование сцены, вывод буфера кадра.
m_pImpl->Clear();
const float deltaSeconds = chronometer.GrabDeltaTime();
OnUpdateWindow(deltaSeconds);
OnDrawWindow(m_pImpl->GetWindowSize());
CUtils::ValidateOpenGLErrors();
m_pImpl->SwapBuffers();
chronometer.WaitNextFrameTime(FRAME_PERIOD);
}
}
Финальная версия
Реализацию можно улучшить: сейчас цветки имеют одинаковый цвет, который также можно задать случайным распределением. Для этого придётся определить новый тип распределения, который получает два glm::vec3 в качестве границ диапазона и интерполирует их покомпонентно путём соединения трёх линейных распределений типа float.
Подумайте, как ещё можно улучшить систему частиц. Для начала возьмите полный пример к уроку на github. Вот так он выглядит:
