Все статьи Знакомство с C++ и Unit-тестированием
В этой статье мы освоим технику TDD, работу с git и github, немного познакомимся с языком C++ и Фреймворком unit-тестирования Catch2
Следуйте инструкциям. В конце выполните задание, указанное в тексте.
Создаём каталог проекта
Перейдите в каталог, в котором у вас есть права записи (желательно, чтобы в имени каталога не было пробелов и кириллических символов).
Создайте каталог, в котором вы будете размещать свои проекты. Его можно назвать, например, “lw1” (laboratory work 1)
В Visual Studio Code откройте этот каталог. Для этого используйте меню “File”>”Open Folder…”.
Теперь вы можете добавить новый файл в каталог прямо из Visual Studio Code. Попробуйте, это так просто!
Пишем первую программу
Создайте каталог try_catch и в нём создайте файл main.cpp. Добавьте в файл код функции main.
#include <iostream>
int main()
{
std::cout << "Hello, World!" << "\n";
}
Обратите внимание, что функция
mainвозвращает типint— она возвращает операционной системе целочисленный код (0 в случае успешного выполнения, ненулевой код в случае ошибки выполнения). Стандарт C++ разрешает ничего не возвращать из функции main, что мы и сделали.
Теперь надо скомпилировать код. Откройте встроенный терминал Visual Studio Code горячей клавишей “Ctrl+`” либо через меню:
Запустите команду g++ --version, чтобы проверить, что компилятор C++ доступен и функционирует. Результат будет выглядеть примерно так:
>gcc --version
gcc (Ubuntu 7.2.0-1ubuntu1~16.04) 7.2.0
Copyright (C) 2017 Free Software Foundation, Inc.
This is free software; see the source for copying conditions. There is NO
warranty; not even for MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE
Перейдите в терминале в ранее созданный каталог try_catch. Это можно сделать командой cd try_catch. Если команду не удалось выполнить, введите команду dir, чтобы выяснить, какие подкаталоги находятся в текущем каталоге терминала. Сориентируйтесь и добейтесь, чтобы у вас был каталог try_catch с файлом main.cpp.
Теперь запустите сборку программы командой g++ main.cpp -o try_catch. Если всё в порядке, то компилятор ничего не напишет — а случае ошибки компилятор написал бы информацию о причине ошибки.
После этого вы можете запустить консольную команду try_catch — так вы запустите собранную вами программу.
>try_catch
Hello, World!
Ошибки компилятора
Компилятор и отладчик — ваши верные друзья и товарищи: они могут многое рассказать о причинах ошибки в программе. Давайте спровоцируем ошибку и посмотрим, что компилятор скажет о ней!
Замените идентификатор cout на coutt:
#include <iostream>
int main()
{
std::coutt << "Hello, World!" << "\n";
}
Запустите команду компиляции g++ main.cpp -o try_catch
Теперь компилятор вывел сообщение: это список ошибок, возникших при компиляции
main.cpp: In function ‘int main()’:
main.cpp:5:10: error: ‘coutt’ is not a member of ‘std’
std::coutt << "Hello, World!" << "\n";
^~~~~
main.cpp:5:10: note: suggested alternative: ‘cout’
std::coutt << "Hello, World!" << "\n";
^~~~~
cout
Давайте разберём текст ошибки подробно:
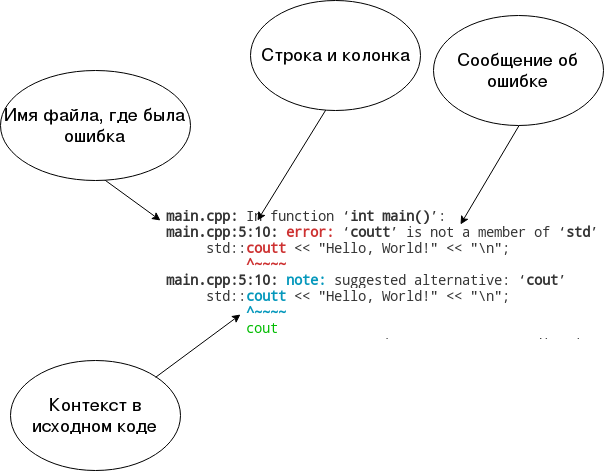
Вы можете заметить, что компилятор точно определил причину ошибки и даже предложил способ исправления для случая, если это была просто опечатка.
Всегда читайте сообщения об ошибках, если только не научились определять ошибку с одного взгляда.
Разработка через тестирование
TDD (Test Driven Development) - это подход к написанию кода, при котором перед реализацией какой-либо функциональности пишутся тесты для неё. При таком подходе разработка, например, нового класса происходит циклически, метод за методом:
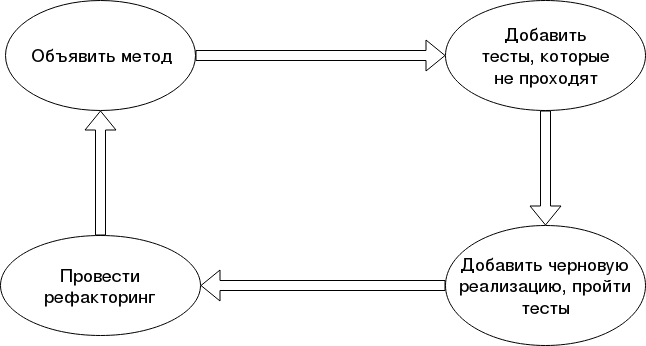
Смысл подхода в том, что ещё до написания какого-либо кода реализации класса вы сразу создаёте подушку безопасности: модульные тесты, проверяющие работоспособность основных сценариев использования метода или класса. Под прикрытием тестов вы можете спокойно переписывать код класса — и не бояться его сломать: любое нарушение функциональности будет обнаружено уже написанными тестами.
Через TDD удобно разрабатывать код, который трудно протестировать вручную: обработку строк, математические вычисления, классы для организации асинхронного кода и т.д.
Мы разработаем через тестирование класс для работы с вектором из двух элементов. Но перед этим освоим Фреймворк модульного тестирования.
Готовимся тестировать
Для тестирования мы будем использовать Фреймворк Catch2, который можно загрузить в виде одного заголовочного файла: github.com/catchorg/Catch2/blob/master/single_include/catch.hpp
Загрузите этот файл. Создайте каталог libs и поместите туда загруженный файл catch.hpp.
Для старта протестируем простейшую функцию, вычисляющую квадрат целого числа. Ознакомьтесь с её будущей реализацией, но пока не добавляйте в свой код:
// ! НЕ ДОБАВЛЯЙТЕ ЭТОТ ПРИМЕР В СВОЙ КОД !
// Определение функции Square, возвращающей квадрат заданного целого числа.
int Square(int value)
{
return value * value;
}
Добавьте в файл main.cpp объявление этой же функции, пока без определения:
int Square(int value);
Объявление не содержит кода, реализующего функцию, но уже резервирует (с точки зрения компилятора) заданное имя как имя функции. После объявления вы уже можете вызывать функцию — правда, программу не получится собрать, пока где-нибудь в вашем коде не появится определение функции, либо не появится внешняя библиотека, реализующая эту же функцию.
Теперь удалите функцию main и добавьте в начале файла подключение заголовка Catch2:
// Макрос заставит Catch самостоятельно добавить определение функции main()
// Это можно сделать только в одном файле
#define CATCH_CONFIG_MAIN
#include "../libs/catch.hpp"
Снова соберите программу командой g++ main.cpp -o try_catch — сборка должна пройти успешно (без сообщений).
Теперь добавьте объявление тест-кейса.
TEST_CASE("Squares are computed", "[Square]")
{
REQUIRE(Square(1) == 1);
REQUIRE(Square(2) == 4);
REQUIRE(Square(3) == 9);
REQUIRE(Square(7) == 49);
REQUIRE(Square(10) == 100);
}
Это объявление интенсивно использует макросы. Перед компиляцией компилятор заменит все макросы в соответствии с их объявлением, то есть макрос
TEST_CASE(...)будет заменён, скорее всего, на объявление функции, реализующий тест кейс, и код регистрации этой функции в общем наборе тестов. МакросREQUIREбудет заменён на проверяемое сравнение значений.
Попробуйте собрать программу — и у вас не получится! Посмотрите на текст ошибки. В нём сказано, что нет ссылки на Square(int). Это значит, что компоновщик, автоматически вызванный компилятором, смог найти вызовы функции Square, но нигде не смог найти машинный код этой функции. Машинного кода нет, потому что нет и исходного кода — мы разместили только объявление функции без определения.
Давайте теперь реализуем функцию Square неправильно. Замените объявление функции на следующее определение:
int Square(int value)
{
return 1;
}
Соберите программу. Затем запустите программу try_catch в терминале. Вы увидит сообщения об ошибке в тестах!

Давайте теперь напишем черновую, но работоспособную версию Square:
int Square(int value)
{
int square = value;
square = square * value;
return square;
}
Соберите программу и запустите её в терминале. Все тесты будут успешно пройдены:

Но разве это повод останавливаться? Конечно, нет: код функции Square пока ещё далёк от идеала. Его можно сократить, убрав явно излишнюю переменную square:
int Square(int value)
{
return value * value;
}
Снова соберите программу и запустите её в терминале. Все тесты будут успешно пройдены:

Только что вы освоили ценный навык: рефакторить код под прикрытием тестов. Если тестов нет, то случайная опечатка или забывчивость в процессе правок могут сломать страшный на вид, но работоспособный код. Под прикрытием тестов поломка будет обнаружена. Этот эффект особенно заметен в динамических языках (вроде JavaScript или Python), но и в C++ вы можете избавиться от мучительной отладки, если просто будете писать автоматические тесты для некоторых задач — таких, как обработка строк, файлов или математические вычисления.
Структура Vector2f
Создайте каталог vector2, и в нём два файла: main.cpp и Vector2f.hpp
Мы напишем структуру, которая будет хранить декартовы координаты вектора из двух элементов (x, y). Мы могли бы объявить эту сущность как класс, а не структуру, тем более что в C++ между ключевыми словами class и struct практически нет разницы. Но C++ Core Guidelines не советуют так делать:
C.2: Use class if the class has an invariant; use struct if the data members can vary independently
Вектор не имеет внутреннего инварианта: его элементы могут быть изменены независимо друг от друга. Поэтому мы объявим его как структуру. Поместите это объявление в файл “Vector2f.hpp”:
#pragma once
// pragma once защищает от проблемы двойного включения заголовка в файл
// подробнее: https://stackoverflow.com/questions/1143936/
// Подключаем заголовок cmath из стандартной библиотеки, он пригодится позже
// Документация заголовка: http://en.cppreference.com/w/cpp/header/cmath
#include <cmath>
// Объявляем новый тип данных - структуру с названием Vector2f
struct Vector2f
{
// Два поля структуры имеют тип float
// Мы явно указываем, что поля в любом случае надо инициализировать нулём.
// Использование неинициализированной памяти - одна из самых страшных
// ошибок C++ программиста, и её надо всячески избегать.
float x = 0;
float y = 0;
// Конструктор без аргументов инициализирует структуру в той
// инструкции, где она объявлена. Нас устраивает реализация
// конструктора, предлагаемая компилятором по умолчанию,
// поэтому мы написали "= default"
Vector2f() = default;
// Конструктор с двумя аргументами инициализирует структуру
// двумя значениями. Пример:
// Vector2 speed(10, 20);
Vector2f(float x, float y)
: x(x), y(y)
{
}
};
// После объявления структуры следует поставить точку с запятой.
// Если этого не сделать, возникнет ошибка компиляции.
// Некоторые компиляторы плохо обрабатывают эту ошибку и выдают
// много индуцированных ошибок вместо одной правильной.
Теперь протестируем конструктор нашего класса — да, от этого мало пользы, но надо же с чего-то начать!
Перепишите этот код в main.cpp:
// Макрос заставит Catch самостоятельно добавить определение функции main()
// Это можно сделать только в одном файле
#define CATCH_CONFIG_MAIN
#include "../libs/catch.hpp"
// Включаем заголовок, где мы описали структуру
#include "Vector2f.hpp"
// В C++ есть много способов вызвать один и тот же конструктор.
// Мы попробуем большинство из них.
TEST_CASE("Can be constructed", "[Vector2f]")
{
// Обычное конструирование при объявлении.
Vector2f v1(1, 2);
REQUIRE(v1.x == 1);
REQUIRE(v1.y == 2);
// Явный вызов конструктора, затем присваивание.
Vector2f v2 = Vector2f(-1, 29);
REQUIRE(v2.x == -1);
REQUIRE(v2.y == 29);
// Конструирование списком инициализации (C++11) - более универсальный приём.
Vector2f v3 = { 5, -11 };
REQUIRE(v3.x == 5);
REQUIRE(v3.y == -11);
// Универсальное конструирование (C++11) - ещё более универсальное
Vector2f v4{ 18, -110 };
REQUIRE(v4.x == 18);
REQUIRE(v4.y == -110);
}
Для сборки программы достаточно собрать один только “main.cpp”, заголовочные файлы сборке не подлежат, т.к. директива #include в любом случае на время компиляции включает содержимое указанного файла в текущий файл (в нашем случае “main.cpp”).
Перейдите в терминале в каталог “vector2” командой cd ..\vector2
Затем соберите программу командой g++ main.cpp -o vector2 и запустите её. Все тесты должны быть пройдены.
Добавляем метод length
Метод — эта функция, связанная с объектом. В C++ объект, связанный с методом, передаётся при вызове неявно и доступен через ключевое слово this. Впрочем, оно нам пока не потребуется: все поля объекта также доступны в методе напрямую.
Длина вектора, согласно теореме Пифагора, вычисляется как квадратный корень из суммы квадратов компонентов вектора. Это справедливо не только для вектора из 2 элементов, но и для векторов любых размерностей.
Для вычисления длины вектора нам нужно уметь извлекать квадратный корень. Это умеет делать функция std::sqrt. Прочитайте её документацию, затем взгляните на реализацию метода length:
// ..внутри объявления Vector2f
float length() const
{
return std::sqrt(x * x + y * y);
}
Вы внимательно прочитали документацию sqrt? В каких случаях в sqrt возникает ошибка? Может ли такая ситуация произойти в функции length?
Теперь пора протестировать метод:
TEST_CASE("Can compute length", "[Vector2f]")
{
// Пифагоровы числа: 3, 4, 5
Vector2f v1 = {3.f, 4.f};
REQUIRE(v1.length() == 5.f);
// Пифагоровы числа: 12, 35, 37
Vector2f v2 = {12.f, 35.f};
REQUIRE(v2.length() == 37.f);
}
Здесь мы использовали опасный приём: сравнение чисел типа float. Из-за погрешностей при работе с числами с плавающей запятой тесты вполне могут провалиться. Для сравнения чисел с плавающей точкой Catch2 предоставляет вспомогательный класс Approx, которым мы воспользуемся:
TEST_CASE("Can compute length", "[Vector2f]")
{
// Пифагоровы числа: 3, 4, 5
Vector2f v1 = {3.f, 4.f};
REQUIRE(v1.length() == Approx(5.f));
// Пифагоровы числа: 12, 35, 37
Vector2f v2 = {12.f, 35.f};
REQUIRE(v2.length() == Approx(37.f));
// Пифагоровы числа: 85 132 157
Vector2f v3 = {85.f, -132.f};
REQUIRE(v3.length() == Approx(157.f));
// Пифагоровы числа: 799 960 1249
Vector2f v4 = {799.f, -960.f};
REQUIRE(v4.length() == Approx(1249.f));
// Пифагоровы числа: 893 924 1285
Vector2f v5 = {893.f, -924.f};
REQUIRE(v5.length() == Approx(1285.f));
}
Теперь, когда мы протестировали метод “length”, финальным штрихом будет рефакторинг. Иногда стандартная библиотека C++ предоставляет не только базовые средства вроде sqrt, но и продвинутые, подходящие для более конкретных случаев. Функция std::hypot может вычислить гипотенузу по двум катетам, то есть тот же самый корень из суммы квадратов компонентов вектора.
Замените реализацию Vector2f::length() на предложенную ниже, соберите программу и запустите её, чтобы повторить все тесты и убедиться, что старая и новая реализации работают одинаково.
float length() const
{
return std::hypot(x, y);
}
Добавляем оператор сложения
Язык C++ позволяет применять операторы +, -, *, /, &&, || и т.д. не только к примитивным типам int, unsigned, bool, float и т.д., но и к пользовательским типам данных. Для этого в языке есть механизм перегрузки операторов. Этим механизмом мы и воспользуемся.
Оператор может быть реализован с помощью метода, и его определение можно разместить внутри класса. Обратите внимание, что
- есть две формы оператора: обычный
+и дополняющий (augmented)+=; различие в том, что первый оператор возвращает новое значение, а второй оператор добавляет правое выражение к старому значению левого выражения - обычный оператор не меняет значение экземпляра структуры, поэтому он помечен ключевым словом
const - в языке принято из дополняющего оператора возвращать ссылку на сам объект, чтобы вы могли писать конструкции вида
x = y += 5(хотя писать такой код не рекомендуется)
Сначала добавим наивную реализацию:
Vector2f operator+(const Vector2f& other) const
{
return { 0, 0 };
}
Vector2f& operator+=(const Vector2f& other)
{
// Разыменование указателя this позволяет объекту получить ссылку на себя
// Оператор не константный, поэтому и ссылка не константная
return *this;
}
Добавим модульные тесты, соберём и запустим программу. Тесты должны пройти завершиться с ошибкой.
TEST_CASE("Can sum vectors", "[Vector2f]")
{
Vector2f v1 = Vector2f{3, 5} + Vector2f{5, -5};
REQUIRE(v1.x == 8);
REQUIRE(v1.y == 0);
Vector2f v2 = Vector2f{11, -6} + Vector2f{-6, 11};
REQUIRE(v2.x == 5);
REQUIRE(v2.y == 5);
Vector2f v3 = Vector2f{11.2f, -6.71f} + Vector2f{-6.2f, 11.72f};
REQUIRE(v3.x == Approx(5.f));
REQUIRE(v3.y == Approx(5.01f));
}
Теперь можно реализовать операторы сложения, запустить тесты снова и увидеть результат:
Vector2f operator+(const Vector2f& other) const
{
return { x + other.x, y + other.y };
}
Vector2f& operator+=(const Vector2f& other)
{
x += other.x;
y += other.y;
return *this;
}
Добавляем функцию для скалярного произведения
Расчёт скалярного произведения — это, как и сложение, бинарная операция над векторами. Однако, для скалярного произведения нет общепринятого символа (иногда используют символ умножения, но это может привести к путанице). Поэтому мы не станем создавать оператор скалярного произведения.
В англоязычной литературе скалярное произведение обозначают фразой “dot product” или словом “dot” — его мы будем использовать. Однако, стоит ли добавлять метод dot? Если мы это сделаем, код пользователя нашего класса будет выглядеть примерно так:
Vector2f a = { 2, 5 };
Vector2f b = { -3, 1 };
Vector2f c = a.dot(b);
Сразу возникает вопрос: почему в этом выражении “a” важнее, чем “b”? Можно ли поменять операнды местами? Являются ли они равнозначными?
Чтобы не создавать путаницы, мы откажемся от метода и напишем свободную функцию dot. Чтобы соблюсти One Definition Rule (ODR), мы добавим ключевое слово inline.
Термин “свободная функция” означает, что функция не является методом и не находится внутри определения какой-либо структуры или класса. Эта функция не связана ни с какими объектами и полностью свободна.
inline float dot(const Vector2f& a, const Vector2f& b)
{
return 0;
}
Теперь добавим тесты, соберём программу и запустим её. Тесты должны провалиться.
TEST_CASE("Calculates dot product", "[Vector2f]")
{
float d1 = dot(Vector2f{3, 5}, Vector2f{5, -5});
REQUIRE(d1 == -10);
float d2 = dot(Vector2f{11, -6}, Vector2f{6, 11});
REQUIRE(d2 == 0);
float d3 = dot(Vector2f{-1, 1}, Vector2f{-3, 2});
REQUIRE(d3 == 5);
}
Остановимся и оглянемся назад
Только что вы освоили технику TDD, которая позволяет легко наращивать код, выполняющий математические вычисления, операции над строками и файлами и другие подобные вещи. Вы также познакомились с базовым синтаксисом языка C++, не вникая в глубокие детали вроде шаблонов C++, constexpr или noexcept.
Теперь пришло время помочь своим товарищам: если кто-то ещё не закончил предыдущий этап или закопался в проблемах, нужно его откопать!
Разрабатываем в команде класс Vector3f
Теперь вам нужно в команде разработать класс Vector3f, имеющий целый ряд операторов и свободных функций.
Здесь находится исходный код, с которого можно начать разработку: github.com/ps-group/dive-into-cpp. Вам нужно:
- зарегистрироваться на github
- создать fork этого репозитория через веб-интерфейс github
- клонировать (git clone) репозиторий
- перейти в каталог “vector3” и собрать тесты командой
g++ Vector3f_tests.cpp -o vector3, затем запустить “vector3”
Далее в цикле, пока весь класс не будет реализован:
- определиться с коллегами, какой оператор, метод или функцию возьмёте на себя вы
- разработать оператор/метод/функцию по принципам TDD
- добавить изменения в индекс git командой
git add <файл> - зафиксировать изменения, сделав commit (git commit)
- отправить изменения на удалённый репозиторий (git push origin)
- в интерфейсе github создать pull request
Напомним ещё раз, как выглядит цикл TDD:

Приступайте!