Все статьи Знакомство с OpenGL
В статье мы познакомимся со стандартом OpenGL и напишем простейшее приложение, использующее API OpenGL.
Клонируем репозиторий, создаём ветку
Для освоения OpenGL мы будем использовать репозиторий с примерами cg-course-2018/QtLabs2D. Если вы ещё не клонировали к себе этот репозиторий, клонируйте его. После этого вы можете переключиться на ветку stable в интерфейсе своего клиента git или в консоли.
Вы должны переключиться в существующую ветку, а не в новую. Возможно, перед началом потребуется синхронизировать репозитории (
git fetch origin).
git checkout stable
Теперь на основе ветки stable создайте ветку tmp_{NAME}, где вместо {NAME} — ваше имя на латинице.
git checkout -b tmp_sergey
Ветку не нужно будет отправлять на удалённый репозиторий. Она временная.
Что такое OpenGL
OpenGL — это стандарт API для рисования трёхмерной графики. В нашем курсе будем использовать OpenGL 3.x — примерно то же самое, что GLES 2.x или WebGL 1.
Посмотрите на общую историю версий графических API, чтобы понять, где мы находимся:
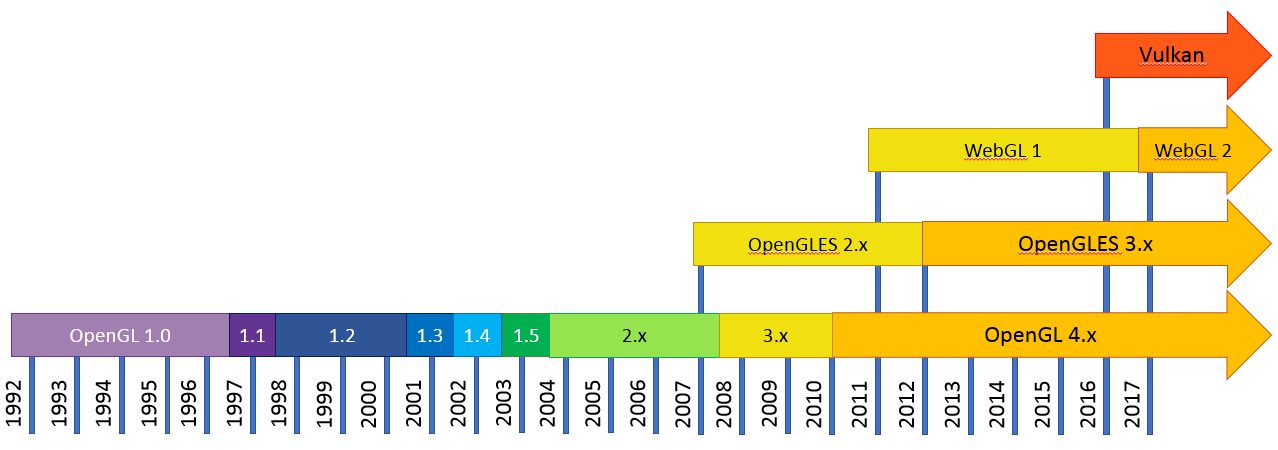
За годы, прошедшие между OpenGL 1.x и OpenGL 3.x, представления программистов о 3D-графике изменились кардинально. Было обнаружено, что программный интерфейс, разработанный для OpenGL 1.0, имеет недостаточную гибкость и потворствует потерям производительности при рисовании графики. Начиная с OpenGL 3.0, была представлена полностью новая модель программирования с использованием OpenGL, а старый способ был объявлен устаревшим.
В последующие годы появились очередные новшества, такие как OpenGL 4.x и Vulkan. Они нацелены на сверхбыстрый параллелизм при вычислениях и на нестандартные применения видеокарт (например, для выполнения расчётов общего назначения с помощью Computing Shaders). Если же вы хотите изучить именно графику, не стоит оглядываться на OpenGL 4 и Vulkan: их использование даже в минимальных примерах требует прекрасного понимания 3D-графики, умения качественно писать многопоточный и асинхронный код, глубоких знаний в системном программировании.
OpenGL спроектирован для видеокарт
Это означает, что в OpenGL приложениях изображение рисует не центральный процессор, а множество узкоспециализированных процессоров внутри видеокарты. В редких случаях используется медленная программная растеризация: в этом случае изображение рисует центральный процессор в несколько потоков.
Современные видеокарты предоставляют огромные вычислительные возможности благодаря параллельной обработке вершин и фрагментов. Это хорошо показано на видео “CPU vs GPU” от NVIDIA:
Возможности OpenGL на конкретном компьютере зависят от операционной системы и от производителя драйвера. OpenGL на Linux и на Windows имеют разные возможности. OpenGL в драйверах от NVIDIA и в драйверах от Intel также различаются. Тем не менее, можно писать код, одинаково качественно работающий на любой реализации OpenGL — для этого нужно соблюдать стандарты и внимательно читать документацию используемых функций OpenGL.
Создаём сцену для работы с OpenGL
В наборе проектов QtLabs2D из шаблона Qt GUI Application создайте новый проект приложения с названием “Sample05”:
Удалите все файлы, кроме “main.cpp”. Перейдите к настройкам проекта и добавьте в пути поиска заголовочных файлов путь к корню репозитория. Это можно сделать, используя переменную SolutionDir:
$(SolutionDir);$(IncludePath)
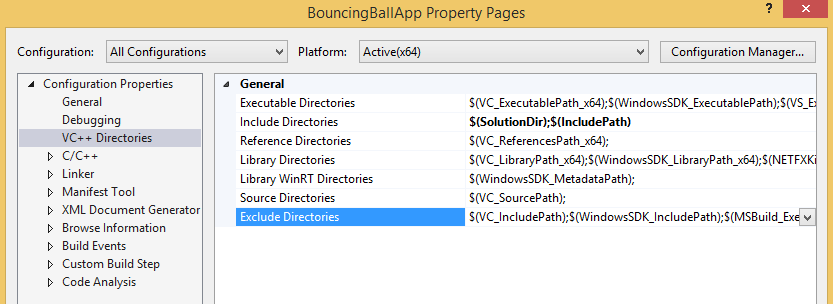
Затем нужно добавить ссылку на проект libplatform, чтобы система сборки автоматически выполняла компоновку с ним.
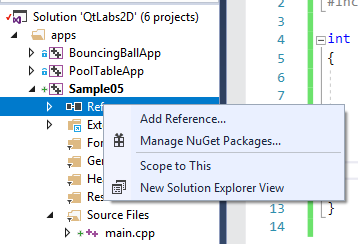
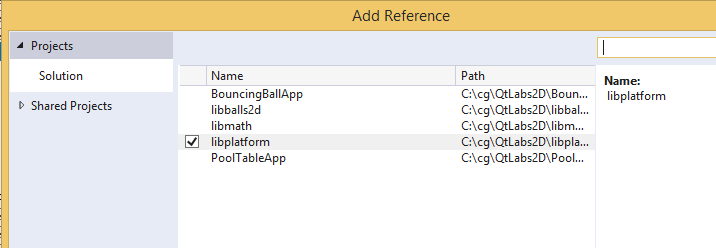
Затем перепишите в “main.cpp” следующий код:
#include <QtWidgets/QApplication>
#include <QtWidgets/QMessageBox>
#include <libplatform/libplatform.h>
#include <iostream>
int main(int argc, char *argv[])
{
QApplication app(argc, argv);
try
{
// Окно размером 800x600, используем OpenGL Core Profile
platform::RenderWindowOptions opts = { 800, 600, true };
platform::RenderWindow window(opts);
window.show();
return app.exec();
}
catch (const std::exception &ex)
{
std::cerr << ex.what() << std::endl;
QMessageBox::warning(
nullptr,
QLatin1String("Sample05"),
QString::fromUtf8(ex.what()));
}
}
Наконец, соберите и запустите проект “Sample05”. Программа должна собраться успешно, после запуска программы отобразится окно размерами 800x600 (вероятно, залитое чёрным цветом).
Теперь создадим и подключим класс сцены. Создайте в проекте заголовок и “*.cpp” файл для класса SimpleScene.
В заголовке “SimpleScene.h” вам нужно подключить заголовок <libplatform/IRenderScene.h>, и затем перегрузить методы интерфейса IRenderScene:
class SimpleScene : public platform::IRenderScene
{
public:
SimpleScene();
void initialize() final;
void update(float deltaSeconds) final;
void redraw(unsigned width, unsigned height) final;
};
Реализация класса пока что будет пустой:
#include "SimpleScene.h"
SimpleScene::SimpleScene()
{
}
void SimpleScene::initialize()
{
}
void SimpleScene::update(float deltaSeconds)
{
(void)deltaSeconds;
}
void SimpleScene::redraw(unsigned width, unsigned height)
{
(void)width;
(void)height;
}
Теперь можно передать объект класса сцены объекту окна. В функции main добавьте соответствующую инструкцию:
window.setScene(std::make_unique<SimpleScene>());
Путаница версий OpenGL
Интерфейс OpenGL состоит из функций и констант. В новых версиях OpenGL старые функции и константы исчезали (в режиме Core Profile) либо оставались в роли устаревших (в режиме Compatibility Profile).
Для использования OpenGL предоставляется заголовок <GL/gl.h>. Какую версию OpenGL вы увидите в этом заголовке?
- На Windows: OpenGL 1.1, API 1997-го года
- На Android/iOS: зависит от версии NDK/SDK
- На Linux/Mac OSX: зависит от способа подключения заголовка (набора макросов) и версии ОС
Реализацию OpenGL предоставляет видеодрайвер. Это означает, что на Windows с современной видеокартой NVIDIA вам может быть доступна последняя версия OpenGL, а с древней видеокартой — только версия 2.0 или даже 1.1.
На современных Linux/Mac OSX ситуация лучше: если видеокарта устаревшая, то новые возможности OpenGL буду эмулироваться программно. Это работает медленнее и нагружает центральный процессор, зато вам доступна новая версия OpenGL.
Как использовать OpenGL без привязки к версии платформы? Для этой в Qt5 есть класс QOpenGLFunctions_3_3_Core (и серия похожих классов). Вы можете унаследовать от него свой класс сцены
class SimpleScene
: public platform::IRenderScene
, private QOpenGLFunctions_3_3_Core
{
// ...
};
Также добавьте инициализацию функций OpenGL в метод initialize:
void SimpleScene::initialize()
{
QOpenGLFunctions_3_3_Core::initializeOpenGLFunctions();
}
Устанавливаем glm
Подробное описание vcpkg и список пакетов можно найти здесь: blogs.msdn.microsoft.com/vcblog/2016/09/19/vcpkg-a-tool-to-acquire-and-build-c-open-source-libraries-on-windows
Для установки библиотек мы будем использовать пакетный менеджер vcpkg. Пакетный менеджер vcpkg распространяется в исходниках и собирается на машине разработчика. Для сборки потребуется установленная Visual Studio с инструментами C++ разработчика.
Порядок установки описан в консольных командах:
:: Клонируем репозиторий vcpkg (ветка master)
git clone https://github.com/Microsoft/vcpkg
:: Переходим в каталог клона репозитория
cd vcpkg
:: Выполняем скрипт для сборки vcpkg
bootstrap-vcpkg.bat
:: Теперь в корне репозитория лежит vcpkg.exe, который можно вызывать
:: из каталога либо добавить в переменную окружения PATH.
После того, как вы получили vcpkg.exe, вы можете устанавливать пакеты командой install.
В частности, нам потребуется установить GLBinding и GLM:
vcpkg install glbinding:x64-windows glm:x64-windows
В команде, представленной выше, имена пакетов перечисляются по порядку, а в качестве суффикса используется так называемый “триплет”: имя_пакета:триплет.
- Имя пакета задаёт одно из множества имён доступных библиотек, полный список есть в блоге Visual C++ Team
- Триплет задаёт архитектуру и режим сборки
Доступные триплеты:
x86-windows
x64-windows-staticx
x86-windows
x86-windows-static
arm-uwp
x64-uwp
x86-uwp
Для удобства использования пакетов vcpkg вы можете включить режим интеграции для всех проектов на своей машине одной командой:
vcpkg integrate install
Как работает OpenGL
В основном OpenGL оперирует треугольниками, изображениями и состояниями драйвера рисования. Если упростить схему работы, останется пять ключевых шагов рисования каждого объекта на экране. Рассмотрим все эти шаги.
Шаг №1 - загрузка вершин примитивов
Программист передаёт из управляющей программы массивы данных, описывающих вершины графических примитивов, то есть треугольников, линий или точек (чаще всего треугольников). Каждая фигура и каждая поверхность будет нарисована с помощью примитивов. На рисунке показано, как разбить сектор эллипса на треугольники:
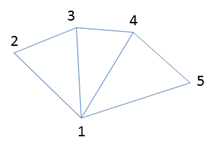
Шаг №2 - обработка вершин примитивов вершинным шейдером
На втором шаге выполняется вершинный шейдер (англ. vertex shader): он получает на вход все данные одной из вершин, а на выход обязан предоставить четырёхкомпонентный вектор с координатами вершины и набор любых других данных для фрагментного шейдера:
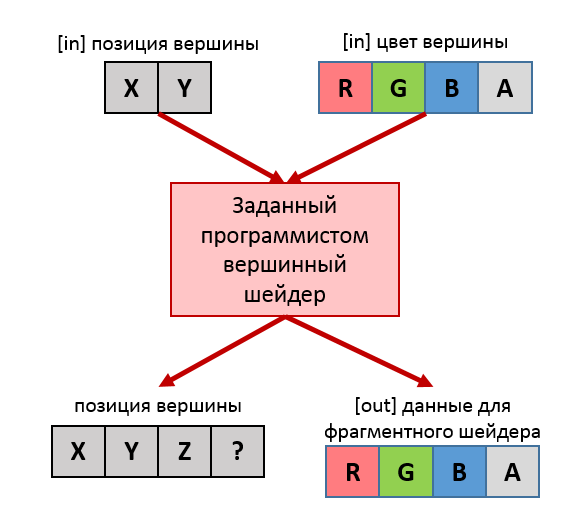
Программист заранее указывает свой вершинный шейдер. Его пишут на специальном языке GLSL, затем он компилируется видеодрайвером и выполняется прямо на видеокарте.
Шаг №3 - интерполяция атрибутов вершин и фрагментация примитивов
Представьте, что вы рисуете треугольник на клетчатой бумаге. Какие-то клетки будут зарисованы полностью, другие — только частично, а оставшиеся не будут зарисованы вообще. Точно так же видеокарта должна определить, в какие пиксели попадает треугольник. Эти пиксели называются фрагментами.
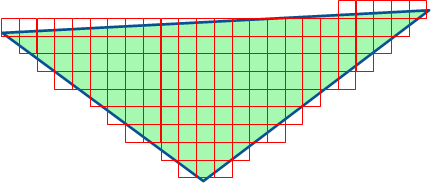
Представьте, что вы захотели сделать треугольник разноцветным, с плавным переходом от жёлтого цвета по левому краю в красный цвет на правом. В OpenGL это выполняется автоматически:
- вы указываете разные цвета для каждой из вершин треугольника
- на шаге №3 видеокарта выполняет в каждом фрагменте линейную интерполяцию, вычисляя взвешенное значение цвета или любого другого атрибута
Линейная интерполяция — это интерполяция с линейным (равномерным) изменением свойства от вершины A к вершине B. Возьмём условный параметр t ∈ [0..1], описанный следующим образом:
- для фрагмента, содержащего вершину A,
t = 0 - для фрагмента, содержащего вершину B,
t = 1 - для фрагмента, лежащего между A и B ровно посередине,
t = 0.5 - и так далее для всех фрагментов между A и B
Линейно интерполированное свойство фрагмента будет вычисляться по формуле: p(t) = pA ∙ (1 - t) + pB ∙ t. Легко заметить, что эта формула работает для самих вершин A и B:
- для вершины A:
p(0) = pA ∙ (1 - 0) + pB ∙ 0 = pA - для вершины B:
p(1) = pA ∙ (1 - 1) + pB ∙ 1 = pB
Конечный результат линейной интерполяции RGBA-цвета от вершин по всему треугольнику показан на рисунке:

Шаг №4 - обработка фрагментов фрагментным шейдером
На данном шаге снова вызывается пользовательский код в составе фрагментного шейдера (англ. fragment shader). Его также пишут на языке GLSL. Фрагментный шейдер получает на вход всё, что вершинный шейдер ему передал, но в преобразованном виде. Допустим, вершинный шейдер сохранил для фрагментного цвет вершины — но фрагментный шейдер оперирует фрагментами, и поэтому переданные данные также проходят линейную интерполяцию.
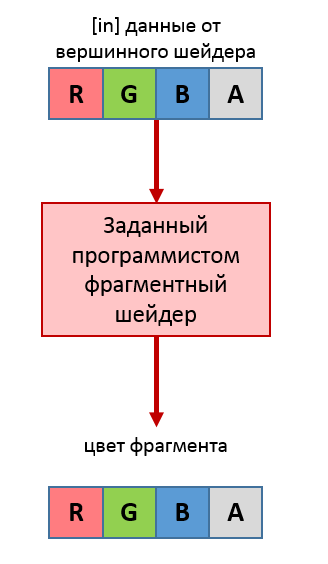
Шаг №5 - проверки, смешивание цвета и запись в буфер кадра
На последнем шаге фрагмент проходит ряд тестов — в каждом из них видеокарта проверяет, должен ли фрагмент попасть в кадр. Например, в 3D пространстве фрагмент может быть закрыт другим геометрическим телом, и это выявляется в тесте глубины (англ. depth test).
Если проверка пройдена (что в 2D графике случается почти всегда), то фрагмент записывается в пиксель кадра. Перед эти выполняется смешивание, позволяющее наложить полупрозрачный пиксель на существующий фон кадра.
Конвейер в целом
Все шаги конвейера изображены на единой схеме, взятой из статьи An intro to modern OpenGL. Chapter 1: The Graphics Pipeline:

Подготовка: RandomColorGenerator
Чтобы продемонстрировать работу интерполяции атрибутов вершин, мы будем генерировать цвета вершин случайным образом. Для этого создайте класс RandomColorGenerator. Объявление будет следующим:
#pragma once
#include <glm/vec4.hpp>
#include <vector>
#include <random>
class RandomColorGenerator
{
public:
RandomColorGenerator();
glm::vec4 GenerateColor();
private:
// Палитра цветов для выбора.
std::vector<glm::vec4> m_palette;
// random_device - это источник непредсказуемых псевдослучайных чисел.
std::random_device m_rd;
// mt19937 - это "Вихрь Мерсенна", он размножает одно псевдослучайное число,
// превращая в несколько по известному алгоритму.
std::mt19937 m_generator;
// В линейном случайном распределении вероятность появления
// каждого из чисел одинакова.
std::uniform_int_distribution<size_t> m_indexDist;
};
Реализация генератора случайных цветов будет всего лишь выбирать цвет из готовой палитры:
#include "RandomColorGenerator.h"
namespace
{
std::vector<glm::vec4> MakePalette()
{
// Превращает rgb(255, 0, 128) в vec4{ 1, 0, 0.5, 1 }
auto rgb = [](unsigned red, unsigned green, unsigned blue) {
return glm::vec4(float(red) / 255.f, float(green) / 255.f, float(blue) / 255.f, 1);
};
// Цвета подобраны на сайте https://websafecolors.info/color-chart
return {
rgb(0, 204, 102),
rgb(102, 102, 102),
rgb(102, 153, 204),
rgb(153, 255, 153),
rgb(204, 153, 51),
rgb(0, 255, 102),
rgb(204, 0, 102),
rgb(204, 102, 255),
rgb(102, 255, 255),
rgb(153, 255, 102),
};
}
}
RandomColorGenerator::RandomColorGenerator()
: m_palette(MakePalette())
, m_generator(m_rd())
, m_indexDist(0, m_palette.size() - 1u)
{
}
glm::vec4 RandomColorGenerator::GenerateColor()
{
const size_t index = m_indexDist(m_generator);
return m_palette.at(index);
}
Запускаем конвейер
Перейдите к “SimpleScene.cpp” и добавьте подключение заголовков glm. Заголовки пригодятся нам для работы с векторной алгеброй.
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>
#include <glm/vec2.hpp>
Создайте анонимное пространство имён и добавьте в него константы-строки, содержащие исходные коды вершинного и фрагментного шейдеров.
Анонимное пространство имён прячет константы и функции от других единиц трансляции (cpp-файлов), тем самым избавляя вас от неожиданных конфликтов имён функций.
namespace
{
// Этот вершинный шейдер выполняет две задачи:
// 1) передаёт цвет фрагментному шейдеру
// 2) выполняет ортографическое проецирование вершины,
// по сути проецируя вершину на плоскость экрана.
const char kVertexShaderCode[] = R"**(#version 110
in vec2 i_position;
in vec4 i_color;
out vec4 v_color;
uniform mat4 u_projection_matrix;
void main()
{
v_color = i_color;
gl_Position = u_projection_matrix * vec4( i_position, 0.0, 1.0 );
}
)**";
// Этот фрагментный шейдер устанавливает фрагменту переданный из
// вершинного шейдера цвет.
static const char kFragmentShaderCode[] = R"**(#version 110
in vec4 v_color;
void main()
{
gl_FragColor = v_color;
}
)**";
} // anonymous namespace
Компиляция шейдеров
Что такое шейдер? Это маленькая программа на языке GLSL (расшифровывается OpenGL Shading Language). Задача программы зависит от типа шейдера: вершинный шейдер трансформирует вершины, фрагментный шейдер вычисляет цвет фрагмента фигуры. Шейдер работает как чистая функция: один вход, один выход и никаких состояний (вы не можете ничего запомнить между двумя вызовами шейдера).
Компиляция шейдера выполняется во время выполнения вашей программы. Компилятор шейдеров находится в ядре видеодрайвера. Руководит компиляцией ваша программа. В OpenGL разделены понятия “шейдер” и “программа”. Программа состоит из нескольких разнотипных шейдеров. Минимальная программа в OpenGL Core Profile состоит из вершинного и фрагментного шейдеров.
Общая схема компиляции шейдеров изображена ниже.
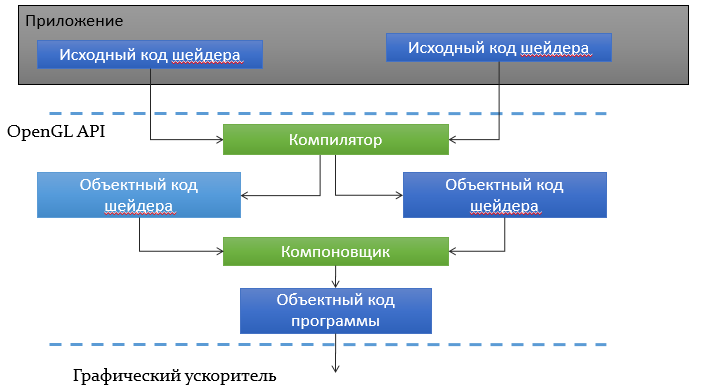
Для сборки шейдера мы будем использовать API OpenGL. Примерная схема вызовов (без обработки ошибок) выглядит следующим образом:
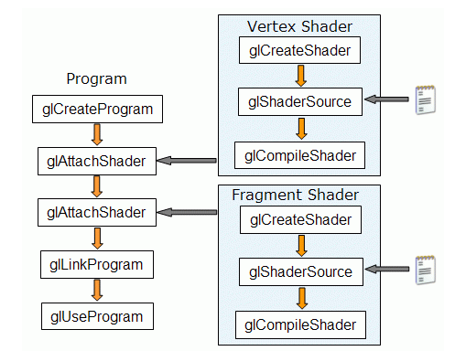
Добавьте классу SimpleScene три поля:
GLuint m_vertexShader = 0;
GLuint m_fragmentShader = 0;
GLuint m_program = 0;
После этого в метод initialize() добавьте вызов нового приватного метода initializeShaders(), в котором будет размещена компиляция шейдеров и компоновка программы:
void SimpleScene::initializeShaders()
{
m_vertexShader = compileShader(GL_VERTEX_SHADER, kVertexShaderCode);
m_fragmentShader = compileShader(GL_FRAGMENT_SHADER, kFragmentShaderCode);
m_program = linkProgram({ m_vertexShader, m_fragmentShader });
}
Приватный метод compileShader будет выполнять компиляцию шейдера и проверку статуса компиляции:
GLuint SimpleScene::compileShader(GLenum type, const std::string & source)
{
// Выделяем ресурс шейдера
GLuint shader = glCreateShader(type);
// Передаём исходный код шейдера видеодрайверу
const auto length = static_cast<int>(source.length());
const char* sourceLine = source.data();
glShaderSource(shader, 1, (const GLchar**)&sourceLine, &length);
// Просим видеодрайвер скомпилировать шейдер и проверяем статус
glCompileShader(shader);
GLint ok = 0;
glGetShaderiv(shader, GL_COMPILE_STATUS, &ok);
if (ok == GL_FALSE)
{
// При неудаче есть лог ошибок, который мы соберём
// и в первую очередь надо узнать длину лога.
GLint logLength = 0;
glGetShaderiv(shader, GL_INFO_LOG_LENGTH, &logLength);
// Зная длину, выделяем строку нужного размера и копируем в неё лог
std::string log(logLength, '\0');
GLsizei ignored = 0;
glGetShaderInfoLog(shader, log.size(), &ignored, (GLchar*)log.data());
// Бросаем исключение, прикрепив к нему лог
throw std::runtime_error("shader compilation failed: " + log);
}
return shader;
}
Приватный метод linkProgram выполняет компоновку программы из шейдеров:
GLuint SimpleScene::linkProgram(const std::vector<GLuint>& shaders)
{
// Запрашиваем у видеодрайера новый объект.
GLuint obj = glCreateProgram();
// Прикрепляем ранее скомпилированные шейдеры.
for (GLuint shader : shaders)
{
glAttachShader(obj, shader);
}
// Просим видеодрайвер выполнить компоновку и проверяем статус.
glLinkProgram(obj);
GLint status = 0;
glGetProgramiv(obj, GL_LINK_STATUS, &status);
if (status == GL_FALSE)
{
// При неудаче есть лог ошибок, который мы соберём
// и в первую очередь надо узнать длину лога.
GLint logLength = 0;
glGetProgramiv(obj, GL_INFO_LOG_LENGTH, &logLength);
// Зная длину, выделяем строку нужного размера и копируем в неё лог
std::string log(logLength, '\0');
GLsizei ignored = 0;
glGetProgramInfoLog(obj, log.size(), &ignored, (GLchar*)log.data());
// Бросаем исключение, прикрепив к нему лог
throw std::runtime_error("program linking failed " + log);
}
return obj;
}
В конце добавьте в деструктор SimpleScene удаление шейдерной программы и шейдеров:
SimpleScene::~SimpleScene()
{
glDeleteProgram(m_program);
glDeleteProgram(m_vertexShader);
glDeleteProgram(m_fragmentShader);
}
Вершинные данные
В старых версиях OpenGL существовали стандартные атрибуты (свойства) вершин: координаты, текстурные координаты, цвет и так далее. Однако, стандартизация ограничивала возможности программиста. Поэтому в современном OpenGL вершина может иметь какие угодно числовые или векторные величины, описывающие её содержимое. Способ интерпретации вершинных данных вы определяете самостоятельно в шейдерах.
Наши шейдеры ожидают два атрибута на каждую вершину: двумерные координаты и четырёхмерный цвет (RGBA). Поэтому мы поместим в начале заголовка “SimpleScene.h” определение структуры, которую мы назовём VertexP2C4:
struct VertexP2C4
{
glm::vec2 xy;
glm::vec4 rgba;
};
Далее мы должны сообщить драйверу видеокарты смещения атрибутов вершины в памяти. Дело в том, что на видеокарту мы будем загружать целые массивы вершин, и внутри массива будут так называемые interleaved массивы атрибутов. Другими словами, несколько массивов атрибутов как будто бы сплетены в единый массив вершинных данных:
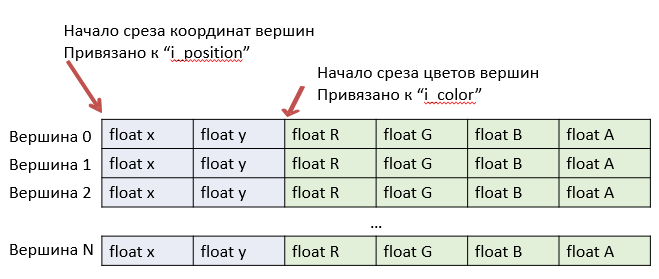
Во время компиляции шейдера видеодрайвер назначил каждому атрибуту его собственный целочисленный идентификатор. Мы должны получить у шейдерной программы идентификаторы атрибутов, а затем для каждого атрибута указать смещения в памяти, с помощью которых OpenGL сможет в непрерывном массиве памяти найти нужные байты. Этим займётся приватный метод bindVertexData:
void SimpleScene::bindVertexData(const std::vector<VertexP2C4> &verticies)
{
// OpenGL должен получить байтовые смещения полей относительно структуры VertexP2C4.
const void *colorOffset = reinterpret_cast<void *>(offsetof(VertexP2C4, rgba));
const void *posOffset = reinterpret_cast<void *>(offsetof(VertexP2C4, xy));
const size_t stride = sizeof(VertexP2C4);
// Привязываем атрибут i_color к данным в вершинном буфере.
const int colorLocation = glGetAttribLocation(m_program, "i_color");
glEnableVertexAttribArray(colorLocation);
glVertexAttribPointer(colorLocation, glm::vec4().length(), GL_FLOAT, GL_FALSE, stride, colorOffset);
// Привязываем атрибут i_position к данным в вершинном буфере.
const int posLocation = glGetAttribLocation(m_program, "i_position");
glEnableVertexAttribArray(posLocation);
glVertexAttribPointer(posLocation, glm::vec2().length(), GL_FLOAT, GL_FALSE, stride, posOffset);
// Загружаем данные в вершинный буфер.
glBufferData(GL_ARRAY_BUFFER, stride * verticies.size(), verticies.data(), GL_STATIC_DRAW);
}
Vertex Buffer Object и Vertex Array Object
Vertex Buffer Object - это объект видеодрайвера, представляющий область пользовательских данных на видеокарте. Для программиста VBO доступен в виде целочисленного идентификатора.
Чтобы хранить целочисленный идентификатор VBO, добавьте в SimpleScene поле GLuint m_vbo = 0;.
Кроме того, мы будем хранить Vertex Array Object - объект, позволяющий оптимизировать смену состояний видеодрайвера. Пока что мы используем VAO просто потому, что OpenGL требует хотя бы одного VAO, поэтому добавьте в класс ещё одно поле: GLuint m_vao = 0;
Затем в функцию initialize добавьте инициализацию VBO и VAO:
// Создаём Vertex Buffer Object (VBO) для загрузки данных,
// в этот буфер мы запишем параметры вершин для видеокарты.
glGenBuffers(1, &m_vbo);
glBindBuffer(GL_ARRAY_BUFFER, m_vbo);
// Создаём Vertex Array Object (VAO), который хранит связи между данными
// в VBO и переменными шейдера.
glGenVertexArrays(1, &m_vao);
glBindVertexArray(m_vao);
В конце добавьте деструктор классу SimpleScene, который будет очищать данные:
SimpleScene::~SimpleScene()
{
glDeleteProgram(m_program);
glDeleteProgram(m_vertexShader);
glDeleteProgram(m_fragmentShader);
glDeleteBuffers(1, &m_vbo);
glDeleteVertexArrays(1, &m_vbo);
}
Триангуляция пятиугольника
Среди всех многоугольников в компьютерной графике предпочитают выпуклые многоугольники (англ. convex), т.к. их проще всего разделить на треугольники. Согласно википедии:
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Благодаря этому мы можем разделить выпуклый многоугольник на треугольники с помощью центральной точки. Таким образом мы создадим своего рода веер треугольников.

Следует учесть, что многие вершины будут продублированы — каждая внешняя вершина входит в состав двух треугольников, но при этом треугольники могут иметь разный цвет, а цвета определяются вершинами.
Добавьте в анонимное пространство имён функции триангуляции многоугольника:
// Генерирует список вершин треугольников для выпуклого многоугольника, заданного вершинами и центром.
// @param center - геометрический центр многоугольника
// @param hullPoints - вершины многоугольника
// @param colorGen - генератор цвета полученных треугольников
std::vector<VertexP2C4> tesselateConvexByCenter(const glm::vec2& center, const std::vector<glm::vec2>& hullPoints, RandomColorGenerator& colorGen)
{
const size_t size = hullPoints.size();
std::vector<VertexP2C4> verticies;
verticies.reserve(3u * size);
for (size_t pointIndex = 0; pointIndex < size; ++pointIndex)
{
// Генерируем цвет треугольника и добавляем три его вершины в список.
const glm::vec4 triangleColor = colorGen.GenerateColor();
const size_t nextPointIndex = (pointIndex + 1) % size;
verticies.push_back({ hullPoints.at(pointIndex), triangleColor });
verticies.push_back({ hullPoints.at(nextPointIndex), triangleColor });
verticies.push_back({ center, triangleColor });
}
return verticies;
}
// Генерирует список вершин треугольников для выпуклого многоугольника, заданного вершинами.
std::vector<VertexP2C4> tesselateConvex(const std::vector<glm::vec2>& verticies, RandomColorGenerator& colorGen)
{
// Центр выпуклого многоугольника - это среднее арифметическое его вершин
const glm::vec2 center = std::accumulate(verticies.begin(), verticies.end(), glm::vec2()) / float(verticies.size());
return tesselateConvexByCenter(center, verticies, colorGen);
}
Триангуляция круга
Разделить круг на треугольники легко с помощью тригонометрии: достаточно пройтись по углам от 0° до 360° с некоторым шагом, например, 1°. Каждый угол вместе с радиусом задаёт точку в полярных координатах.
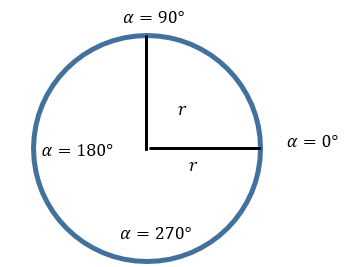
Перевести полярные координаты в декартовы очень легко — достаточно вспомнить одно из определений синуса и косинуса:
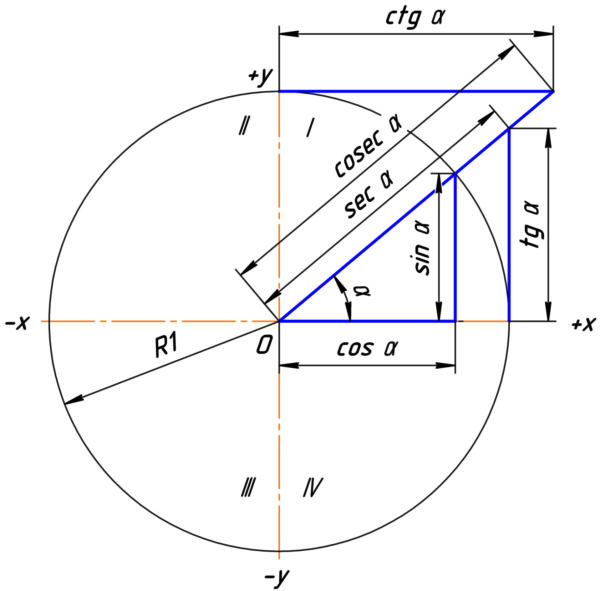
Декартовы координаты по-английски называются Эвклидовыми (euclidean), и мы назовём функцию соответствующе:
// Переводит полярные координаты {radius, angle} в декартовы.
// Угол задаётся в радианах.
glm::vec2 euclidean(float radius, float angle)
{
return { radius * cos(angle), radius * sin(angle) };
}
Теперь мы можем описать функцию для триангуляции круга:
constexpr float PI = 3.1415926f;
glm::vec2 euclidean(float radius, float angle)
{
return { radius * cos(angle), radius * sin(angle) };
}
// Функция делит круг на треугольники,
// возвращает массив с вершинами треугольников.
std::vector<VertexP2C4> tesselateCircle(float radius, const glm::vec2& center, RandomColorGenerator& colorGen)
{
assert(radius > 0);
// Круг аппроксимируется с помощью треугольников.
// Внешняя сторона каждого треугольника имеет длину 2.
constexpr float step = 2;
// Число треугольников равно длине окружности, делённой на шаг по окружности.
const auto pointCount = static_cast<unsigned>(radius * 2 * PI / step);
// Вычисляем точки-разделители на окружности.
std::vector<glm::vec2> points(pointCount);
for (unsigned pi = 0; pi < pointCount; ++pi)
{
const auto angleRadians = static_cast<float>(2.f * PI * pi / pointCount);
points[pi] = center + euclidean(radius, angleRadians);
}
return tesselateConvexByCenter(center, points, colorGen);
}
Выполняем триангуляцию двух фигур
Теперь мы можем триангулировать фигуры, чтобы получить результат, который вы видите на скриншоте:
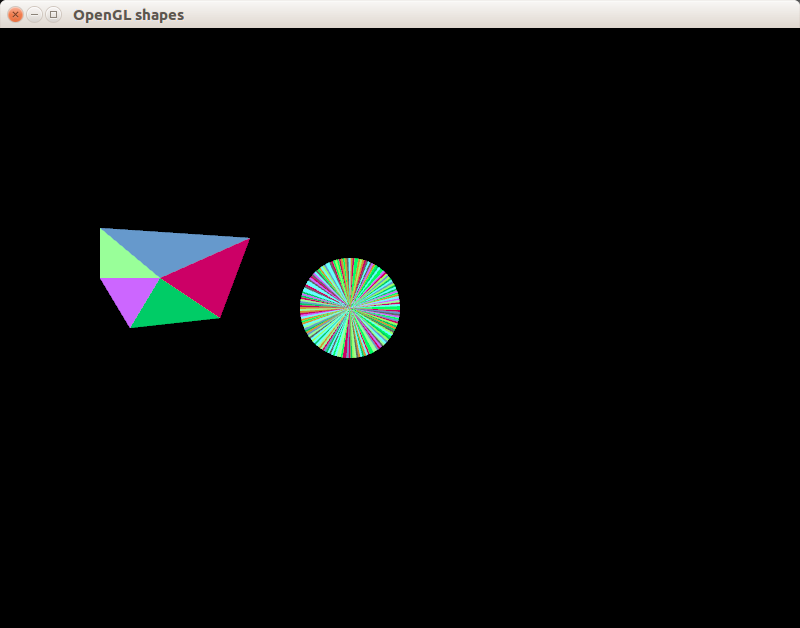
Прежде всего добавьте в SimpleScene новое поле size_t m_vertexCount = 0; - позже число треугольников потребуется нам для рисования.
Добавим в main следующий код в метод initializeShapes, вызов которого надо поместить в конец метода initialize:
void SimpleScene::initializeShapes()
{
// Привязываем вершинный массив
glBindVertexArray(m_vao);
// Генерируем список вершин треугольников, представляющих круг,
// каждый треугольник будет раскрашен в собственный цвет.
RandomColorGenerator colorGen;
std::vector<VertexP2C4> verticies = tesselateCircle(50, { 350, 280 }, colorGen);
// Генерируем список вершин треугольников, представляющих пятиугольник,
// добавляем его к списку вершин круга.
const std::vector<glm::vec2> convexPoints = {
{ 100, 200 },
{ 250, 210 },
{ 220, 290 },
{ 130, 300 },
{ 100, 250 },
};
const std::vector<VertexP2C4> convexVerticies = tesselateConvex(convexPoints, colorGen);
std::copy(convexVerticies.begin(), convexVerticies.end(), std::back_inserter(verticies));
// Выполняем привязку вершинных данных в контексте текущего VAO.
bindVertexData(verticies);
m_vertexCount = verticies.size();
}
Устанавливаем матрицу проецирования
Казалось бы, что может быть проще, чем наложить виртуальные координаты холста на координаты окна? Однако, OpenGL устроен иначе: он рассчитан на 3D графику, в которой координаты виртуального мира не совпадают с координатами окна. Более того, начало координат OpenGL находится в нижнем левом углу, а не в верхнем левом!
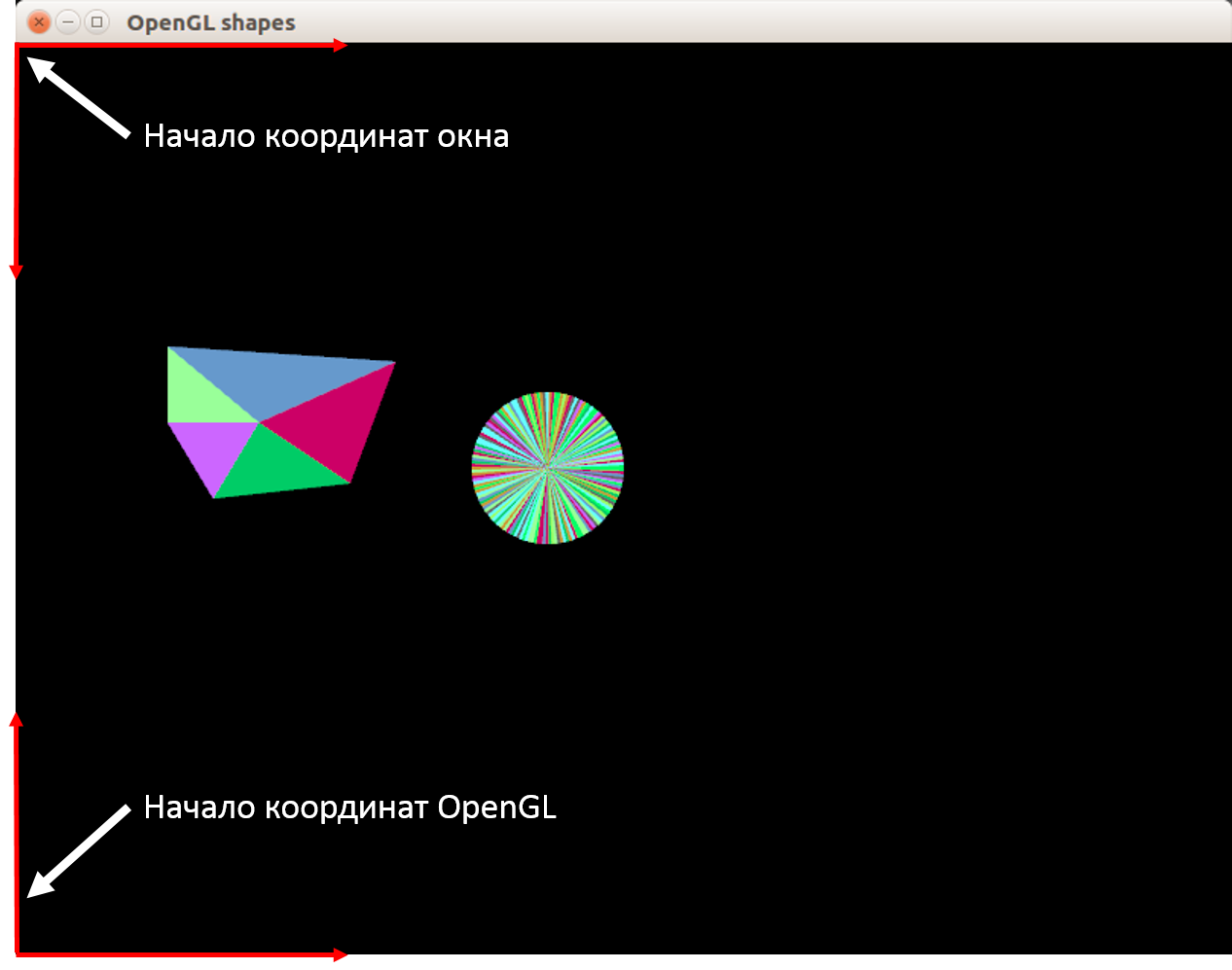
Ради нужд 3D графики все координаты вершин проецируются внутрь куба размерами 2x2x2 условных единиц с помощью матрицы проецирования. Поскольку мы хотим получить 2D координаты, да ещё и совмещённые с привычными координатами окна, нам нужна матрица ортографического проецирования, которая растянет координаты вершин обратно из куба 2x2x2 в координаты окна. Для этой цели мы напишем метод setProjectionMatrix, выполняющий две задачи:
- вычислить матрицу ортографического проецирования из куба на координаты окна с помощью функции glm::ortho
- установить эту матрицу как константу в шейдерной программе с помощью glUniformMatrix4fv
void SimpleScene::setProjectionMatrix(unsigned width, unsigned height)
{
// Вычисляем матрицу ортографического проецирования
const glm::mat4 mat = glm::ortho(0.f, float(width), float(height), 0.f);
// Передаём матрицу как константу в графической программе
glUniformMatrix4fv(glGetUniformLocation(m_program, "u_projection_matrix"), 1, GL_FALSE, glm::value_ptr(mat));
}
Реализуем метод redraw
Метод redraw будет с использованием полученных размеров окна устанавливать так называемый Viewport, привязывать шейдерную программу и VAO, а затем очищать изображение, устанавливать матрицу проецирования, наконец, вызывать glDrawArrays для рисования всех примитивов.
void SimpleScene::redraw(unsigned width, unsigned height)
{
glViewport(0, 0, width, height);
glUseProgram(m_program);
glBindVertexArray(m_vao);
glClear(GL_COLOR_BUFFER_BIT);
// Устанавливаем матрицу ортографического проецирования.
setProjectionMatrix(width, height);
// Рисуем отдельные треугольники, то есть интерпретируем массив вершин
// как тройки вершин треугольников
glDrawArrays(GL_TRIANGLES, 0, m_vertexCount);
}
Теперь вы наконец можете собрать, запустить и увидеть готовый результат!