Трансформации и камеры

Все статьи / Трансформации и камеры

В статье вы научитесь ловко использовать математический аппарат векторов и матриц для анимации объектов и реализации виртуальной камеры.

Клонируем репозиторий, создаём ветку

Для освоения OpenGL мы будем использовать репозиторий с примерами cg-course-2018/QtLabs2D. Если вы ещё не клонировали к себе этот репозиторий, клонируйте его. После этого вы можете переключиться на ветку stable в интерфейсе своего клиента git или в консоли.

git checkout stable

Теперь на основе ветки stable создайте ветку tmp_{NAME}, где вместо {NAME} — ваше имя на латинице. Если ветка уже существовала, удалите её.

git branch -D tmp_sergey
git checkout -b tmp_sergey

Ветку не нужно будет отправлять на удалённый репозиторий. Она временная.

Создаём проект

В наборе проектов QtLabs2D из шаблона Qt GUI Application создайте новый проект приложения с названием “Sample07”. Обратите внимание, что проект должен располагаться в подкаталоге “samples” ради наведения порядка. При создании проекта рекомендуется установить опцию “Precompiled header”:

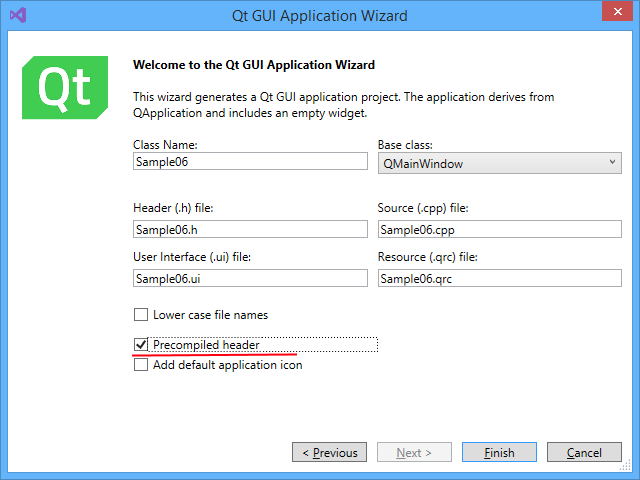
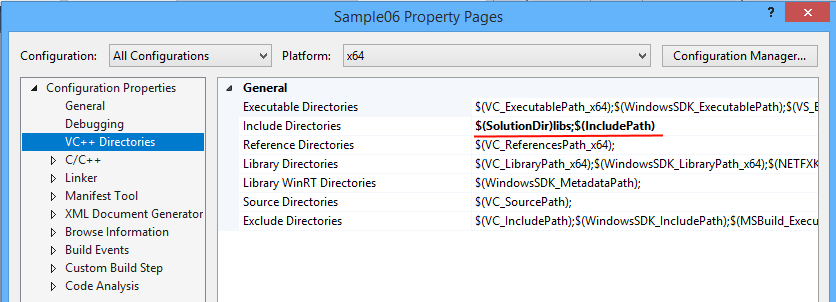
Иллюстрация

Удалите все файлы, кроме “main.cpp”, “stdafx.cpp”, “stdafx.h”. Перейдите к настройкам проекта и добавьте в пути поиска заголовочных файлов путь к подкаталогу “libs” в корне репозитория. Это можно сделать, используя переменную SolutionDir:

$(SolutionDir)libs;$(IncludePath)

Иллюстрация

Затем нужно добавить ссылку на проекты libplatform, libglcore и libmath, чтобы система сборки автоматически выполняла компоновку с ними.

Иллюстрация

Создаём функцию main

Функция main возьмёт на себя следующие задачи:

установка размеров окна и параметров OpenGL
создание окна RenderWindow и сцены AnimatedScene
вывод текста исключения в случае фатальной ошибки

#include "stdafx.h"

#include "AnimatedScene.h"
#include <QtWidgets/QApplication>
#include <QtWidgets/QMessageBox>
#include <iostream>
#include <libplatform/libplatform.h>

int main(int argc, char *argv[])
{
	QApplication app(argc, argv);
	platform::CatchAndDisplay([&] {
		// Окно размером 800x600, используем OpenGL Core Profile и multisampling со значением 8
		QSurfaceFormat format;
		format.setVersion(3, 3);
		format.setSamples(8);
		format.setProfile(QSurfaceFormat::CoreProfile);
		format.setRenderableType(QSurfaceFormat::RenderableType::OpenGL);
		platform::RenderWindowOptions opts = { 800, 600, format };

		platform::RenderWindow window(opts);
		window.setScene(std::make_unique<AnimatedScene>());

		window.show();
		return app.exec();
	});
}

Создаём класс сцены AnimatedScene

Создайте файлы заголовка и реализации класса. Содержимое заголовка будет следующим:

#pragma once
#include "TesselateUtils.h"
#include <libglcore/libglcore.h>
#include <libplatform/IRenderScene.h>

class AnimatedScene
	: public platform::IRenderScene
{
public:
	AnimatedScene();
	~AnimatedScene();

	void initialize() final;
	void update(float deltaSeconds) final;
	void redraw(unsigned width, unsigned height) final;
	bool keyReleaseEvent(platform::IKeyEvent &event) final;

private:
	void bindVertexData(const std::vector<VertexP2C4> &verticies);
	void initializeShaders();
	void setProjectionMatrix(unsigned width, unsigned height);
	void animateShape(std::vector<VertexP2C4> &verticies);
	glm::vec2 animate(const glm::vec2 &point, float phase);

	glcore::ProgramObject m_program;
	glcore::VBO m_vbo;
	glcore::VAO m_vao;

	size_t m_vertexCount = 0;
	float m_totalTime = 0;
};

Обратите внимание на методы keyReleaseEvent и animateShape. Эти методы в дальнейшем будут точками расширения для реализации анимации фигуры и управления камерой.

#include "stdafx.h"
#include "AnimatedScene.h"
#include <algorithm>
#include <glbinding/gl32core/gl.h>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>
#include <glm/vec2.hpp>
#include <libplatform/ResourceLoader.h>

namespace
{
glm::vec2 animateMoveAlongY(const glm::vec2 &point, float phase)
{
	constexpr float kAmplitudePx = 50;
	const float deviation = std::abs(0.5f - phase) / 0.5f;
	return {
		point.x,
		point.y + kAmplitudePx * deviation
	};
}
} // namespace

// Используем функции из gl32core, экспортированные библиотекой glbinding.
using namespace gl32core;

AnimatedScene::AnimatedScene() = default;

AnimatedScene::~AnimatedScene() = default;

void AnimatedScene::initialize()
{
	glcore::initGLBinding();
	initializeShaders();

	m_vao = glcore::createVAO();
	glBindVertexArray(m_vao);

	// Загружаем данные в вершинный буфер.
	m_vbo = glcore::createVBO();
}

void AnimatedScene::update(float deltaSeconds)
{
	m_totalTime += deltaSeconds;
}

void AnimatedScene::redraw(unsigned width, unsigned height)
{
	glViewport(0, 0, width, height);
	glUseProgram(m_program);
	glBindVertexArray(m_vao);

	// Генерируем список вершин треугольников, представляющих полярную розу.
	std::vector<VertexP2C4> verticies = tesselatePolarRose(100.0f, 7, glm::vec2{ 0, 0 }, glm::vec4{ 0.72, 0.2, 1, 0 });
	animateShape(verticies);

	// Загружаем вершины на видеокарту
	glcore::setStreamBufferData(m_vbo, GL_ARRAY_BUFFER, verticies);

	// Выполняем привязку вершинных данных в контексте текущего VAO и VBO.
	glBindBuffer(GL_ARRAY_BUFFER, m_vbo);
	bindVertexData(verticies);

	// Запоминаем число примитивов.
	m_vertexCount = verticies.size();

	glClear(GL_COLOR_BUFFER_BIT);

	// Устанавливаем матрицу ортографического проецирования.
	setProjectionMatrix(width, height);

	glDrawArrays(GL_TRIANGLES, 0, m_vertexCount);
}

bool AnimatedScene::keyReleaseEvent(platform::IKeyEvent &event)
{
	using platform::Key;

	switch (event.getKey())
	{
	case Key::Equal:
		// TODO: zoom camera in.
		break;
	case Key::Minus:
		// TODO: zoom camera out.
		break;
	case Key::Left:
		// TODO: move camera left.
		break;
	case Key::Right:
		// TODO: move camera right.
		break;
	case Key::Up:
		// TODO: move camera up.
		break;
	case Key::Down:
		// TODO: move camera down.
		break;
	}
	return false;
}

void AnimatedScene::initializeShaders()
{
	platform::ResourceLoader loader;

	std::vector<glcore::ShaderObject> shaders;
	shaders.emplace_back(glcore::compileShader(GL_VERTEX_SHADER, loader.loadAsString("draw2d.vert")));
	shaders.emplace_back(glcore::compileShader(GL_FRAGMENT_SHADER, loader.loadAsString("draw2d.frag")));
	m_program = glcore::linkProgram(shaders);
}

void AnimatedScene::bindVertexData(const std::vector<VertexP2C4> &verticies)
{
	// OpenGL должен получить байтовые смещения полей относительно структуры VertexP2C4.
	const void *colorOffset = reinterpret_cast<void *>(offsetof(VertexP2C4, rgba));
	const void *posOffset = reinterpret_cast<void *>(offsetof(VertexP2C4, xy));
	const size_t stride = sizeof(VertexP2C4);

	// Привязываем атрибут i_color к данным в вершинном буфере.
	const int colorLocation = glGetAttribLocation(m_program, "i_color");
	glEnableVertexAttribArray(colorLocation);
	glVertexAttribPointer(colorLocation, glm::vec4().length(), GL_FLOAT, GL_FALSE, stride, colorOffset);

	// Привязываем атрибут i_position к данным в вершинном буфере.
	const int posLocation = glGetAttribLocation(m_program, "i_position");
	glEnableVertexAttribArray(posLocation);
	glVertexAttribPointer(posLocation, glm::vec2().length(), GL_FLOAT, GL_FALSE, stride, posOffset);
}

void AnimatedScene::setProjectionMatrix(unsigned width, unsigned height)
{
	// Вычисляем матрицу ортографического проецирования
	const glm::mat4 mat = glm::ortho(-0.5f * float(width), 0.5f * float(width), -0.5f * float(height), 0.5f * float(height));

	// Передаём матрицу как константу в графической программе
	glUniformMatrix4fv(glGetUniformLocation(m_program, "u_projection_matrix"), 1, GL_FALSE, glm::value_ptr(mat));
}

void AnimatedScene::animateShape(std::vector<VertexP2C4> &verticies)
{
	constexpr float kAnimationPeriodSec = 2.0;
	for (auto &v : verticies)
	{
		const float phase = std::fmod(m_totalTime, kAnimationPeriodSec) / kAnimationPeriodSec;
		assert(phase >= 0.f && phase <= 1.f);
		v.xy = animate(v.xy, phase);
	}
}

glm::vec2 AnimatedScene::animate(const glm::vec2 &point, float phase)
{
	return animateMoveAlongY(point, phase);
}

После добавления сцены проект всё ещё не соберётся - не хватает заголовка TesselateUtils.h. Далее мы создадим его.

Добавляем модуль TesselateUtils

Модуль TesselateUtils будет хранить процедуры, используемые для триангуляции фигур. Таким будет заголовок:

#pragma once

#include <glm/vec2.hpp>
#include <glm/vec4.hpp>
#include <vector>

struct VertexP2C4
{
	glm::vec2 xy;
	glm::vec4 rgba;
};

// Генерирует список вершин треугольников по методу веера треугольников, образованного центром и вершинами фигуры.
//  @param center - геометрический центр многоугольника
//  @param hullPoints - вершины фигуры
//  @param fillColor - цвет полученных треугольников
std::vector<VertexP2C4> tesselateTriangleFan(const glm::vec2 &center, const std::vector<glm::vec2> &hullPoints, const glm::vec4 &fillColor);

// Генерирует список вершин треугольников для выпуклого многоугольника, заданного вершинами.
std::vector<VertexP2C4> tesselateConvex(const std::vector<glm::vec2> &verticies, const glm::vec4 &fillColor);

// Функция делит круг на треугольники,
//  возвращает массив с вершинами треугольников.
std::vector<VertexP2C4> tesselateCircle(float radius, const glm::vec2 &center, const glm::vec4 &fillColor);

// Генерирует список вершин треугольников для фигуры Polar Rose (Полярная Роза),
//  возвращает массив с вершинами треугольников.
//  @param outerRadius - радиус окружности, описывающей полярную розу
//  @param petelsCount - число лепестков, не менее 3
//  @param center - геометрический центр фигуры
//  @param fillColor - цвет полученных треугольников
std::vector<VertexP2C4> tesselatePolarRose(float outerRadius, unsigned petelsCount, const glm::vec2 &center, const glm::vec4 &fillColor);

Реализация будет следующей:

#include "stdafx.h"
#include "TesselateUtils.h"

namespace
{

constexpr float PI = 3.1415926f;

glm::vec2 euclidean(float radius, float angleRadians)
{
	return {
		radius * sin(angleRadians),
		radius * cos(angleRadians)
	};
}

} // namespace

std::vector<VertexP2C4> tesselateTriangleFan(const glm::vec2 &center, const std::vector<glm::vec2> &hullPoints, const glm::vec4 &fillColor)
{
	const size_t size = hullPoints.size();
	std::vector<VertexP2C4> verticies;
	verticies.reserve(3u * size);
	for (size_t pointIndex = 0; pointIndex < size; ++pointIndex)
	{
		// Добавляем три вершины треугольника в список.
		const size_t nextPointIndex = (pointIndex + 1) % size;
		verticies.push_back({ hullPoints.at(pointIndex), fillColor });
		verticies.push_back({ hullPoints.at(nextPointIndex), fillColor });
		verticies.push_back({ center, fillColor });
	}

	return verticies;
}

std::vector<VertexP2C4> tesselateConvex(const std::vector<glm::vec2> &verticies, const glm::vec4 &fillColor)
{
	// Центр выпуклого многоугольника - это среднее арифметическое его вершин
	const glm::vec2 center = std::accumulate(verticies.begin(), verticies.end(), glm::vec2()) / float(verticies.size());
	return tesselateTriangleFan(center, verticies, fillColor);
}

std::vector<VertexP2C4> tesselateCircle(float radius, const glm::vec2 &center, const glm::vec4 &fillColor)
{
	assert(radius > 0);

	// Круг аппроксимируется с помощью треугольников.
	// Внешняя сторона каждого треугольника имеет длину 2.
	constexpr float step = 2;
	// Число треугольников равно длине окружности, делённой на шаг по окружности.
	const auto pointCount = static_cast<unsigned>(radius * 2 * PI / step);

	// Вычисляем точки-разделители на окружности.
	std::vector<glm::vec2> points(pointCount);
	for (unsigned pi = 0; pi < pointCount; ++pi)
	{
		const auto angleRadians = static_cast<float>(2.f * PI * pi / pointCount);
		points[pi] = center + euclidean(radius, angleRadians);
	}

	return tesselateTriangleFan(center, points, fillColor);
}

std::vector<VertexP2C4> tesselatePolarRose(float outerRadius, unsigned petelsCount, const glm::vec2 &center, const glm::vec4 &fillColor)
{
	assert(outerRadius > 0);
	assert(petelsCount >= 3);

	// Фигуры аппроксимируется с помощью треугольников.
	// Внешняя сторона каждого треугольника имеет длину 2.
	constexpr float step = 2;
	// Число треугольников равно длине описанной окружности, делённой на шаг по окружности.
	const auto pointCount = static_cast<unsigned>(outerRadius * 2 * PI / step);

	// Вычисляем точки-разделители на границе фигуры.
	std::vector<glm::vec2> points(pointCount);
	for (unsigned pi = 0; pi < pointCount; ++pi)
	{
		const auto factor = static_cast<float>(petelsCount) / 2.f;
		const auto angleRadians = static_cast<float>(2.f * PI * pi / pointCount);
		const auto radius = static_cast<float>(outerRadius * std::abs(std::cos(factor * angleRadians)));

		points[pi] = center + euclidean(radius, angleRadians);
	}

	return tesselateTriangleFan(center, points, fillColor);
}

Добавляем файлы шейдеров

Теперь мы можем добавить сами шейдеры. Добавлять их можно через шаблон “Text File”, указывая собственное расширение файла:

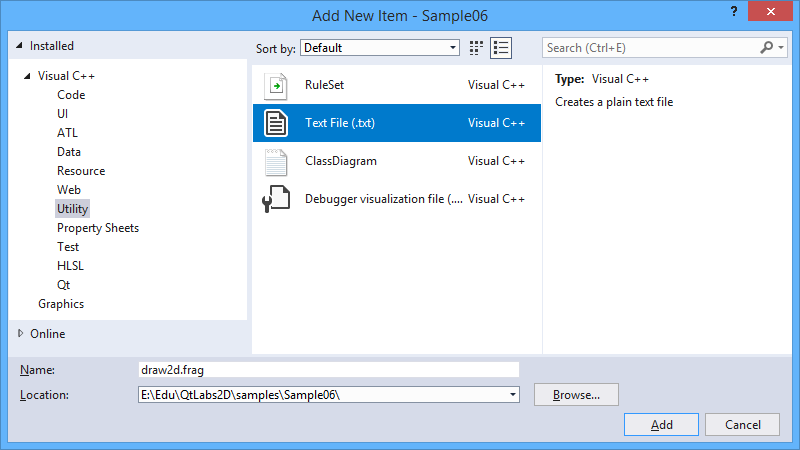
Скриншот

Создайте в проекте файл “draw2d.frag” следующего содержания:

#version 130

in vec4 v_color;
out vec4 out_fragColor;

void main()
{
    out_fragColor = v_color;
}

Создайте в проекте файл “draw2d.vert” следующего содержания:

#version 130

in vec2 i_position;
in vec4 i_color;
out vec4 v_color;
uniform mat4 u_projection_matrix;

void main()
{
	v_color = i_color;
	gl_Position = u_projection_matrix * vec4(i_position.xy, 0.0, 1.0);
}

Добавьте в проект файл “copy_res.bat” следующего содержания:

@echo off
echo Copying resources...

set ProjectDir=%1
set OutDir=%2

echo F | xcopy /Y "%ProjectDir%draw2d.frag" "%OutDir%draw2d.frag"
echo F | xcopy /Y "%ProjectDir%draw2d.vert" "%OutDir%draw2d.vert"

Теперь этот скрипт надо правильно запустить. Перейдите в настройках проекта в раздел “Build Events -> Pre-Link Event” и добавьте команду запуска copy_res.bat "$(ProjectDir)" "$(OutDir)"

переменная ProjectDir будет раскрыта системой сборки в путь к исходному коду проекта
переменная OutDir будет раскрыта системой сборки в путь к выходному каталогу

Иллюстрация

Собираем проект

Соберите и запустите проект. Вы должны получить следующий результат:

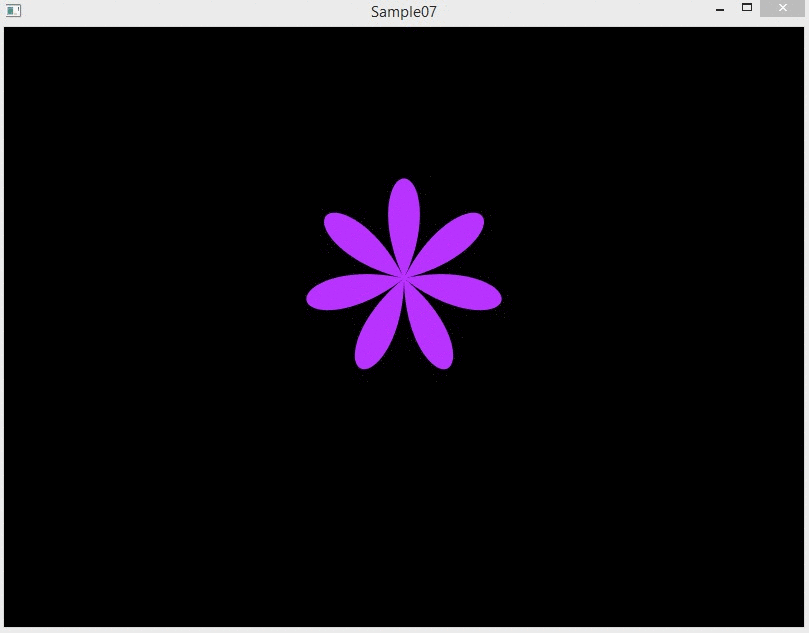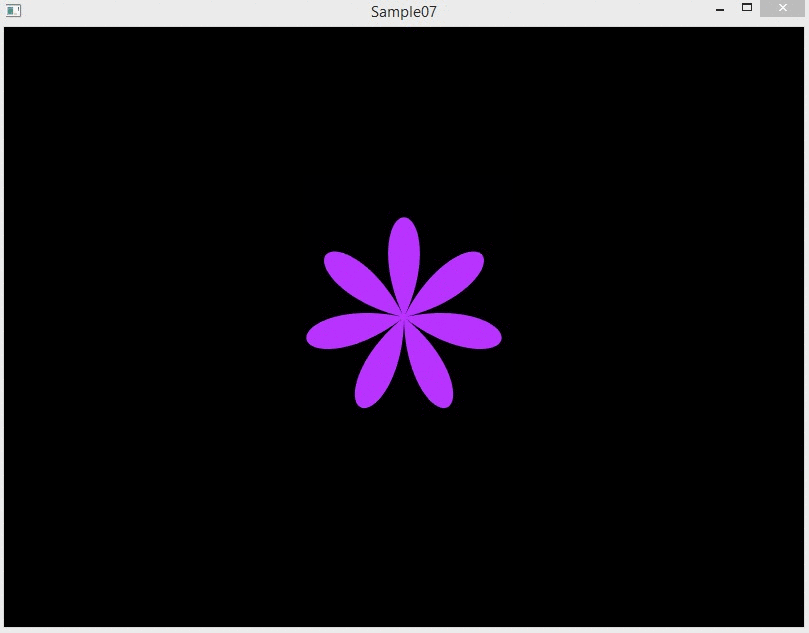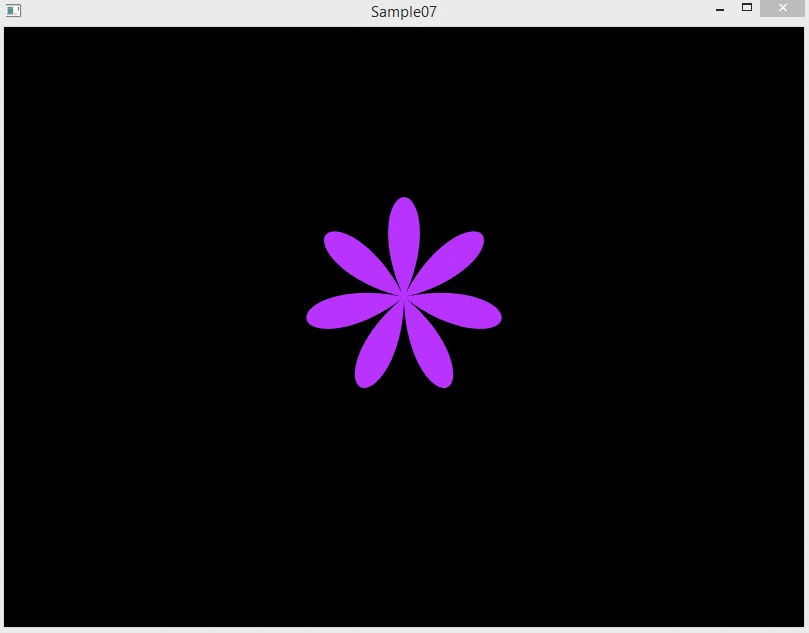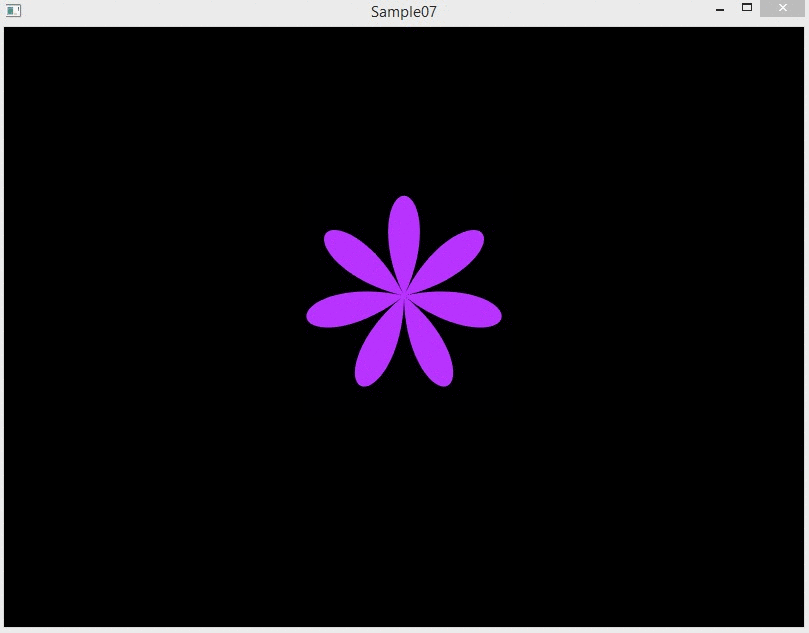
Скриншот

Аффинные преобразования

Аффинные преобразования широко используются в графике, поскольку этот математический аппарат позволяет

из объекта-шаблона нарисовать любое число объектов с любыми размерами, поворотами и местоположениями;
выполнить анимацию составного объекта, моделируя шарнирные и другие крепления частей объекта друг к другу;
реализовать виртуальную камеру, способную поворачиваться, передвигаться и изменять масштаб просмотра.
Любое аффинное преобразование может быть представлено последовательностью трёх элементарных преобразований: масштабирования (scale), поворота (rotate), перемещения (translate), при условии что все операции совершаются относительно начала текущей системы координат.
Аффинное преобразование фигуры выполняется путём применения преобразования ко всем вершинам фигуры
Преобразование можно рассматривать как смену одной системы координат на другую систему координат

Элементарное преобразование scale

Пусть s - вектор, представляющий коэффициенты масштабирования точки по двум осям относительно начала системы координат (коэффициенты для разных осей могут быть разными). Масштабирование точки выполняется следующим образом:

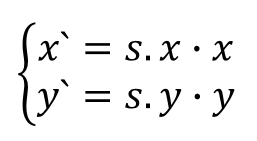
Формула

Можно также выполнить масштабирование вектора путём умножения на матрицу 2x2:

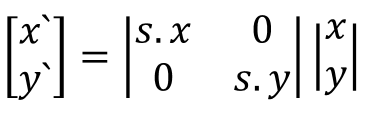
Формула

Напомним, как выполняется умножение матриц. Если мы умножаем M1 на M2 и получаем M3, то:

ширина M3 равна ширине M2, высота M3 равна высоте M1
чтобы вычислить элемент матрицы M3 в колонке №x и строке №y, нужно взять строку №y матрицы M1 и умножить покомпонентно на колонку №x матрицы M2, а затем компоненты полученного вектора сложить, получив скаляр

Задание cg7.1: анимация отражения

С помощью масштабирования можно отразить объект: достаточно масштабировать одну из осей на -1. Напишите свободную функцию glm::vec2 animateFlipY(const glm::vec2& point, float phase), которая будет принимать два параметра

point - вершина, которую надо преобразовать
phase - фаза анимации, в диапазоне [0..1]

Эту функцию вы должны поместить в метод AnimatedScene::animate в качестве реализации анимации.

Требования:

Функция должна масштабировать точку, равномерно изменяя коэффициент масштабирования по оси Y в зависимости от фазы от 1 до -1 и обратно.
Для реализации animateFlipY вы должны написать и использовать функцию glm::vec2 scale2d(const glm::vec2& point, const glm::vec2& s), которая масштабирует точку относительно начала системы координат
- Реализовать масштабирование вы можете любым удобным методом: векторным или матричным
В реализации функций вы не должны использовать функций библиотеки GLM, но можете использовать классы векторов и матриц из этой библиотеки на своё усмотрение

Элементарное преобразование rotate

Пусть 𝜑 - угол вращения (в радианах), на который надо повернуть точку относительно начала системы координат. Вращение точки выполняется следующим образом:

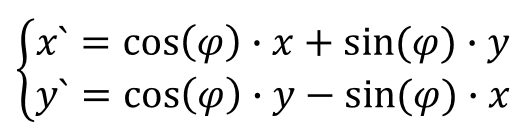
Формула

Можно также выполнить вращение путём умножения на матрицу 2x2:

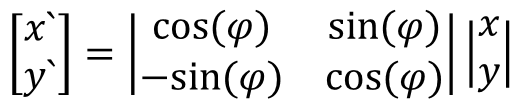
Формула

Задание cg7.2: анимация вращения

Напишите новую свободную функцию glm::vec2 animateRotate(const glm::vec2& point, float phase), которая будет принимать два параметра

point - вершина, которую надо преобразовать
phase - фаза анимации, в диапазоне [0..1]

Эту функцию вы должны поместить в метод AnimatedScene::animate в качестве реализации анимации.

Требования:

Функция должна вращать точку относительно начала координат, равномерно изменяя угол вращения в зависимости от фазы от 0 до 2π и обратно до 0.
Для реализации animateRotate вы должны написать и использовать функцию glm::vec2 rotate2d(const glm::vec2& point, float angleRadians), которая масштабирует точку относительно начала системы координат
- Реализовать вращение вы можете любым удобным методом: векторным или матричным
В реализации функций вы не должны использовать функций библиотеки GLM, но можете использовать классы векторов и матриц из этой библиотеки на своё усмотрение

Элементарное преобразование translate

Пусть t - вектор, представляющий смещения точки относительно начала координат. Тогда смещение точки выполняется следующим образом:

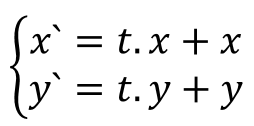
Формула

Матричного представления преобразования translate, на первый взгляд, не существует. Однако, существует трюк, позволяющий представить в виде матриц все три типа аффинных преобразований: это однородные координаты.

Однородные координаты

Вектора и точки на плоскости и в пространстве имеют одно различие:

точка имеет положение
вектор - не имеет

Другими словами, точка привязана к началу координат, а вектор может быть помещён в любом месте. Есть удобный вычислительный трюк, позволяющий единообразно работать с векторами и точками с помощью матриц: достаточно превратить вектор из 2-х координат в вектор из 3-х координат, причём 3-я координата (обозначаемая “w”) будет всегда либо нулём, либо единицей. Для точек 3-я координата равна единице, для векторов, не привязанных к началу координат, 3-я координата равна нулю.

В этом случае матрица translate будет выглядеть следующим образом:

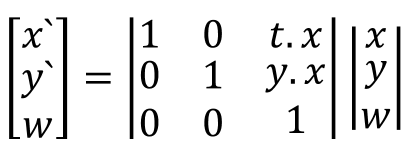
Формула

Если вы умножите эту матрицу на (x y w), третья координата останется неизменной, и это можно интерпретировать следующим образом: точка останется точкой, вектор останется вектором. Нижняя строка в однородном представлении одинакова для всех матриц аффинных преобразований, включая матрицы rotate и scale в однородном представлении.

Комбинировать матрицы в однородном представлении можно, перемножая их. Если, например, вы умножаете матрицу translate на матрицу rotate, вы получите матрицу, которая представляет комплексное преобразование, состоящее из вращения и перемещения. Порядок применения преобразований - обратный к порядку умножения матриц.

Задание cg7.3: комплексная анимация

Напишите новую свободную функцию glm::vec2 animateComplex(const glm::vec2& point, float phase), которая будет принимать два параметра

point - вершина, которую надо преобразовать
phase - фаза анимации, в диапазоне [0..1]

Эту функцию вы должны поместить в метод AnimatedScene::animate в качестве реализации анимации.

Требования:

Функция должна применять комплексную анимацию, эквивалентную последовательному применению следующих преобразований
- масштабирование точки с равномерным изменением коэффициента масштабирования по осям X и Y в зависимости от фазы от 1 до 4 и обратно.
- вращение точки относительно начала координат с равномерным изменением угла вращения в зависимости от фазы от 0 до 2π и обратно до 0.
- движение точки относительно начала координат от 0 до 100px вправо и обратно.
Реализовать комплексное преобразование вы должны методом умножения матриц элементарных преобразований
Для этого вы должны можете использовать функции GLM: rotate, scale, translate; либо вы можете написать свои функции для создания матриц элементарных преобразований
- они находятся в заголовке <glm/gtx/matrix_transform_2d.hpp>
- документацию можно найти на сайте glm.g-truc.net

Задание cg7.4: изменить порядок анимаций

Создайте функцию “animateComplex2”, эквивалентную функции animateComplex во всём, кроме одной детали: элементарные преобразования применяются в обратном порядке. Сравните, как выглядит анимация после изменений.

Если вы всё сделали правильно, то анимация изменится, поскольку умножение матриц не коммутативно, и применение аффинных преобразований также не коммутативно.

Класс Transform2D

Класс Transform2D представляет аффинную трансформацию, состоящую из масштабирования, ориентирующего поворота и перемещения объекта. Этот класс избавит вас от необходимости постоянно помнить о порядке применения преобразований, и облегчит программирование систем, в которых положение, ориентация или даже размеры множества объектов постоянно меняются.

Задание cg7.5: использовать Transform2D

Доработайте функцию animateComplex, чтобы она использовала класс Transform2D для создания преобразования, соответствующего текущей фазе анимации

Задание cg7.6: перенести умножение на матрицу в вершинный шейдер

Перенесите преобразование вершин в вершинный шейдер

добавьте в вершинный шейдер uniform-переменную uniform mat4 u_world_matrix;, в которую вы будете записывать матрицу преобразования
добавьте в вершинный шейдер умножение на u_world_matrix
не забудьте о порядке умножения матриц: преобразование проецирования должно выполняться последним
удалите код, который преобразует каждую вершину фигуры перед заполнением буфера вершин, хранимого на стороне видеокарты
буфер вершин теперь статичный, и вы можете перенести инициализацию буфера в метод AnimatedScene::initialize, тем самым сэкономив на передаче данных видеокарт
добавьте для каждого объекта на сцене в AnimatedScene::redraw вычисление текущей матрицы преобразования с учётом анимации
для этого разберите функцию animate на части, часть выкиньте, а другую часть повторно используйте для определения матрицы преобразования
добавьте в C++ коде передачу значения uniform переменной так же, как это сделано для “u_projection_matrix”, перед вызовом каждой из функций рисования каждого из объектов

Виртуальная камера

Позиция виртуальной камеры — это фактически позиция виртуального наблюдателя, чьим взглядом вы смотрите на 2D сцену сверху. Поворот камеры также эквивалентен повороту виртуального наблюдателя. Масштаб не так просто интерпретировать, поскольку перспективное искажение — термин из трёхмерного пространства; но в любом случае, вы можете связать с камерой масштаб просмотра 2D сцены.

Удивительно, но для реализации виртуальной камеры тоже пригождается механизм аффинных преобразований!

Чтобы изменить положение наблюдателя относительно мира, есть два способа:

преобразовать положение наблюдателя (т.е. передвинуть/повернуть наблюдателя относительно мира)
преобразовать положение каждой вершины виртуального мира (т.е. передвинуть/повернуть мир относительно наблюдателя)

В компьютерной графике выбирают второй способ, поскольку цель первых стадий графического конвейера - получить положение всех вершин виртуального мира относительно наблюдателя.

Преобразование камеры складывается с двумя другими преобразованиями в известную тройку с чётко фиксированным порядком применения:

Преобразование из локальной системы координат объекта в мировую систему координат (т.е. в глобальную систему координат виртуального мира)
Преобразование из мировой системы координат в систему координат наблюдателя
Ортографическое/перспективное преобразование, которое сворачивает трёхмерную сцену OpenGL в куб размерами 2x2x2, легко превращаемый в плоскую картинку

Обратные матрицы - основа обратных преобразований

Преобразование из мировой системы координат в систему координат наблюдателя (с масштабированием или без) может быть выполнено умножением на матрицу. Однако, в вычислении этой матрицы есть нюанс: переход от мировых координат к координатам наблюдателя - это не то же самое, что переход от координат наблюдателя к мировым.

Давайте определимся, как перевести точку из координат наблюдателя в мировые координаты:

Сначала выполним ориентирование, т.е. поворот в соответствии с поворотом наблюдателя
Затем выполним перемещение, т.е. перемещение в соответствии с позицией наблюдателя

Это можно запрограммировать с помощью Transform2D, заполнив его поля и получив матрицу соответствующего преобразования. В виде формул задача будет выглядеть следующим образом:

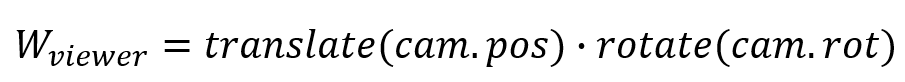
Формула

Любое аффинное преобразование обратимо, и любая матрица аффинного преобразования имеет обратную матрицу. По определению, умножение матрицы на обратную даёт единичную матрицу. Такая матрица не преобразует координаты. В GLM для обращения матрицы есть функция inverse, с её помощью можно получить матрицу преобразования в координаты наблюдателя.

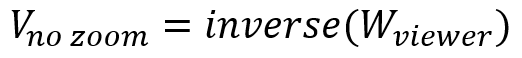
Формула

Остаётся только учесть масштаб: мы можем применить масштабирование после учёта поворота/положения наблюдателя, и это значит, что соответствующую матрицу вам нужно расположить левым операндом умножения матриц.

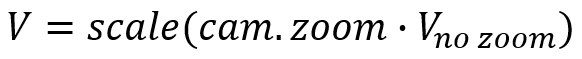
Формула

Задание cg7.7: добавить виртуальную камеру, управляемую горячими клавишами

Доработайте класс AnimatedScene, чтобы в нём хранилось поле Transform2D m_cameraTransform; для хранения преобразования из мировой системы координат в систему координат наблюдателя
- добавьте в вершинный шейдер uniform-переменную uniform mat4 u_view_matrix;, в которую вы будете записывать матрицу преобразования из мировых координат в координаты наблюдателя
- не забудьте о порядке умножения матриц: преобразование проецирования должно выполняться последним, а преобразование из локальных координат в мировые должно происходить до преобразования камеры
- добавьте в C++ коде передачу значения uniform переменной так же, как это сделано для “u_projection_matrix”
- добавьте вместо // TODO: zoom camera in. и других подобных заглушек изменение параметров камеры

Все статьи / Трансформации и камеры

Содержание

Клонируем репозиторий, создаём ветку

Создаём проект

Создаём функцию main

Создаём класс сцены AnimatedScene

Добавляем модуль TesselateUtils

Добавляем файлы шейдеров

Собираем проект

Аффинные преобразования

Элементарное преобразование scale

Задание cg7.1: анимация отражения

Элементарное преобразование rotate

Задание cg7.2: анимация вращения

Элементарное преобразование translate

Однородные координаты

Задание cg7.3: комплексная анимация

Задание cg7.4: изменить порядок анимаций

Класс Transform2D

Задание cg7.5: использовать Transform2D

Задание cg7.6: перенести умножение на матрицу в вершинный шейдер

Виртуальная камера

Обратные матрицы - основа обратных преобразований

Задание cg7.7: добавить виртуальную камеру, управляемую горячими клавишами