Все статьи Шпаргалка по 3D трансформациям средствами GLM
В программировании 3D графики нужны математические приёмы, выходящие за рамки простой арифметики и тригонометрии. В статье мы рассмотрим такие приёмы.
Класс CTransform3D
Для удобства разделения трансформации на части было бы удобно представлять трансформацию трёхмерного объекта не в виде матрицы, а в виде структуры из нескольких составляющих, позволяющих получить матрицу. Такое представление позволяет легко модифицировать отдельные компоненты преобразования, не задевая остальные компоненты.
#pragma once
#include <glm/vec3.hpp>
#include <glm/vec4.hpp>
#include <glm/matrix.hpp>
#include <glm/gtc/quaternion.hpp>
// Преобразует координаты из локальных в мировые в следующем порядке:
// - сначала вершины масштабируются
// например, единичный цилиндр превращается в диск или в трубку
// - затем поворачиваются
// т.е. тела ориентируются в пространстве
// - затем переносятся
// т.е. задаётся положение тела
// изменив порядок, мы изменили бы значение трансформаций.
class CTransform3D
{
public:
// Конструирует трансформацию с
// - единичным масштабированием;
// - нулевым вращением вокруг оси Oy;
// - нулевой позицией.
CTransform3D();
// Преобразует исходную трансформацию в матрицу 4x4.
glm::mat4 ToMat4()const;
glm::vec3 m_sizeScale;
glm::quat m_orientation;
glm::vec3 m_position;
};
Реализация методов данного класса относительно проста. Однако, следует учесть, что компоненты трансформации применяются в строго определённом порядке, при изменении которого компоненты потеряют свой текущий смысл и обретут какой-либо иной — например, компонент поворота, применённый после компонента перемещения, перестанет быть ориентацией тела и станет поворотом вокруг центра.
#include "libchapter4_private.h"
#include "Transform.h"
using namespace glm;
CTransform3D::CTransform3D()
: m_sizeScale(glm::vec3(1))
, m_orientation(glm::angleAxis(0.f, glm::vec3(0, 1, 0)))
{
}
mat4 CTransform3D::ToMat4() const
{
const mat4 scaleMatrix = scale(mat4(), m_sizeScale);
const mat4 rotationMatrix = mat4_cast(m_orientation);
const mat4 translateMatrix = translate(mat4(), m_position);
return translateMatrix * rotationMatrix * scaleMatrix;
}
Понимание матрицы поворотов
Формулы вычисления произвольной матрицы поворота из угла достаточно сложны. Гораздо проще понимать матрицу поворота как объединение трёх векторов направлений: up (вверх), right (вправо) и forward (вперёд):
[ right.x up.x -forward.x 0 ]
[ right.y up.y -forward.y 0 ]
[ right.z up.z -forward.z 0 ]
[ 0 0 0 1 ]
Вектора up, right, forward должны быть взаимно перпендикулярны. Если исходные вектора не перпендикулярны, это можно исправить путём повторного вычисления с помощью нормализованных векторных произведений:
// исходные вектора up и forward, потенциально не перпендикулярные друг другу
// правильным считается вектор forward, и up не совпадает с forward
vec4 up = ...;
vec4 forward = ...;
// вычисляем right как перпендикуляр к плоскости, заданной up и forward
vec4 right = glm::normalize(glm::cross(up, forward));
// вычисляем повторно вектор up как перпендикуляр к плоскости, заданной forward и right
up = glm::normalize(glm::cross(forward, right));
Подобное преобразование производит glm::lookAt, однако, lookAt для установки преобразования в систему координат камеры устанавливает не только вращение, но и перенос.
Повороты (без кватернионов)
Заголовок <glm/gtx/rotate_vector.hpp> предоставляет следующее API:
- поворачивает 2D вектор на заданный угол:
vec2 glm::rotate(vec2 const &v, float angle);
- поворачивает 3D вектор на заданный угол вокруг заданной оси (представленной орт-вектором):
vec3 glm::rotate(vec3 const& v, float angle, vec3 const& normal);
- поворачивают 3D вектор на заданный угол вокруг осей Ox, Oy, Oz соответственно:
vec3 glm::rotateX(vec3 const &v, float angle);
vec3 glm::rotateY(vec3 const &v, float angle);
vec3 glm::rotateZ(vec3 const &v, float angle);
Понимание кватернионов 3D-графике
Произвольную ориентацию трёхмерной поверхности можно задать с помощью одного поворота поверхности вокруг некоторой оси вращения (англ. rotation axis) на некоторый угол вращения (англ. rotation angle):
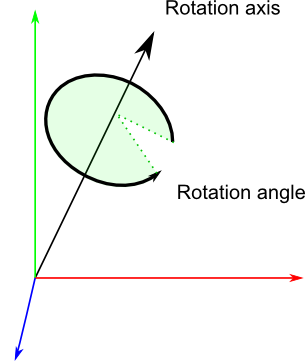
Кватернионом называется четвёрка чисел, вычисляемых из угла поворота и оси вращения по следующим формулам:
// Угол вращения RotationAngle задан в радианах
x = RotationAxis.x * sin(RotationAngle / 2)
y = RotationAxis.y * sin(RotationAngle / 2)
z = RotationAxis.z * sin(RotationAngle / 2)
w = cos(RotationAngle / 2)
Есть другие определения кватернионов, но они сложны и не столь важны в прикладных целях. Показать геометрический смысл кватернионов также трудно. Программисту достаточно знать, что кватернионы дают удобные и общепринятые в графике способы работы с поворотами и ориентацией тел.
Приведём таблицу с примерами значений кватернионов:
| w | x | y | z | Вращение |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | нет вращения |
| 0 | 1 | 0 | 0 | 180° вокруг оси X |
| √0.5 | √0.5 | 0 | 0 | 90° вокруг оси X |
| √0.5 | -√0.5 | 0 | 0 | -90° вокруг оси X |
Переход к кватернионам и обратно
Заголовок <glm/gtc/quaternion.hpp> предоставляет следующее API:
- функция создаёт кватернион на основе оси вращения и угла поворота:
quat glm::angleAxis(float angle, vec3 const& axis);
- с помощью оператора умножения можно применить к вектору вращение, хранимое в кватернионе:
vec3 unrotated = ...;
quat orientation = ...;
vec3 rotated = unrotated * orientation;
- функция превращает кватернион в эквивалентную матрицу поворота:
mat4 glm::mat4_cast(quat const& orientation);
Углы Эйлера и кватернионы
В трёхмерном пространстве любую трансформацию поворота можно представить в виде трёх углов Эйлера. Это возможно благодаря теореме Эйлера, согласно которой любой поворот вокруг произвольной оси можно представить как комбинацию трёх углов, последовательно поворачивающих тело вокруг базовых осей Ox, Oy, Oz.
Тройка углов Эйлера и кватернион являются двумя эквивалентными представлениями некоторой трансформации поворота. Этот факт отражён в GLM:
- конструктор quat, принимающий vec3, формирует кватернион
- функция
glm::eulerAnglesпроводит обратную операцию — получение углов Эйлера из заданного кватерниона
quat(vec3 const& eulerAngles);
vec3 glm::eulerAngles(quat const& quaternion);
Авиационно-космическое представление ориентации
Ориентация в авиационных терминах задаётся тремя углами:
- угол тангажа (англ. pitch, греч. буква θ)

- угол крена (англ. roll, греч. буква ϕ)

- угол рысканья (англ. yaw, греч. буква ψ)

Авиационные углы имеют огромное преимущество — исходные оси Ox, Oy, Oz фиксированы в мировых координатах (или в координатах диспетчерской станции аэропорта), и ориентация камеры задаётся лишь последовательным применением авиационных углов для получения вектора курса полёта (англ. heading):
- сначала считаем курс равным орту оси Ox (т.е. вектору
{1, 0, 0}) - поворачиваем курс на угол рысканья (yaw, ψ) вокруг оси Oy
- вычисляем нормаль к плоскости, образованной вектором курса и вектором Oy (назовём эту нормаль “right”)
- поворачиваем курс на угол тангажа (pitch, θ) вокруг “right”
- вычисляем нормаль к плоскости, образованной вектором курса и вектором “right” (назовём эту нормаль “up”)
- поворачиваем вектор “up” вокруг вектора курса на угол крена (roll, ϕ)
- теперь у нас есть вектор курса (heading, или front) и вектор направления вверх (up), и мы можем использовать уже привычную операцию lookAt для получения матрицы поворота
Данный метод проиллюстрирован на изображении:
Также в GLM есть функции для преобразования между yaw, pitch, roll и другими представлениями:
- функция из заголовочного файла
<glm/gtx/euler_angles.hpp>преобразует углы yaw, pitch, roll в матрицу поворота:
mat4 glm::yawPitchRoll(float yaw, float pitch, float roll);
- функция из заголовочного файла
<glm/gtc/quaternion.hpp>преобразует матрицу поворота в кватернион; соединив её с предыдущей функцией, получим функцию для преобразования yaw, pitch, roll в кватернион:
quat glm::quat_cast(mat4 const& rotationMatrix);
// Пример:
const float yaw = ...;
const float pitch = ...;
const float roll = ...;
const quat orientation = glm::quat_cast(glm::yawPitchRoll(yaw, pitch, roll));
Пересечение луча и объектов
В библиотеке GLM есть заголовок <glm/gtx/intersect.hpp>, который предоставляет средства для поиска пересечения между лучом и геометрическими телами:
- функция intersectRayPlane определяет пересечение луча и плоскости
- функция intersectRaySphere определяет пересечение луча и сферы
- функция intersectRayTriangle определяет пересечение луча и треугольника
- все функции имеют входные параметры, используемые для расчёта, и выходные параметры, такие как дистанция пересечения (от начала луча)
- параметр rayDirection должен быть нормализованным вектором
bool glm::intersectRayPlane(vec3 const& rayOrigin, vec3 const& rayDirection, vec3 const& planeOrigin, vec3 const& planeNormal, float &intersectionDistance);
bool glm::intersectRaySphere(vec3 const& rayOrigin, vec3 const& rayDirection, vec3 const& sphereCenter, float sphereRadiusSquare, float &intersectionDistance);
bool glm::intersectRaySphere(vec3 const& rayOrigin, vec3 const& rayDirection, vec3 const& sphereCenter, float sphereRadiusSquare, vec3 &intersectionPosition, vec3 &intersectionNormal);
bool glm::intersectRayTriangle(vec3 const& rayOrigin, vec3 const& rayDirection, vec3 const& vert0, vec3 const& vert1, vec3 const& vert2, float &baryPosition);
Декомпозиция матрицы 4x4 на составляющие
В GLM есть расширение, позволяющее провести разделение матрицы на базовые аффинные и неаффинные преобразования. Подробнее об этом рассказано:
- в вопросе “glm - Decompose mat4 into translation and rotation?” на stackoverflow
- в документации GLM (glm.g-truc.net)
Расширение подключается заголовком #include <glm/gtx/matrix_decompose.hpp>. Использовать его можно следующим образом:
// входная матрица преобразования
glm::mat4 transformation;
// выходные значения
glm::vec3 sizeScale; // масштабирование, задающее размер
glm::quat orientation; // ориентация тела
glm::vec3 position; // перемещение тела
glm::vec3 skew; // аффинная трансформация сдвига
glm::vec4 perspective; // неаффинное перспективное искажение
// вызов функции декомпозиции
glm::decompose(transformation, sizeScale, orientation, position, skew, perspective);
В некоторых версиях GLM в выходной параметр rotation записывается сопряжённый кватернион ориентации тела вместо ожидаемого значения. Исправить эту проблему можно получением кватерниона, сопряжённого сопряжённому, что даст нам исходный кватернион.
rotation = glm::conjugate(rotation);
Линейная интерполяция чисел, векторов и кватернионов
Линейная интерполяция двух значений вычисляет новое значение как среднее между двумя с заданными значениями с применением весового коэффициента. Формула для обыкновенных чисел очень проста, и она легко масштабируется на векторные величины:
float lerp(float a, float b, float weight)
{
// Ключевой момент: сумма коэффициентов `weight` и `1 - weight` равна 1.
return a * weight + b * (1 - weight);
}
Представьте, как зелёная точка движется между красной и синей; математически это движение описывается изменением весового коэффициента от 0 до 1:
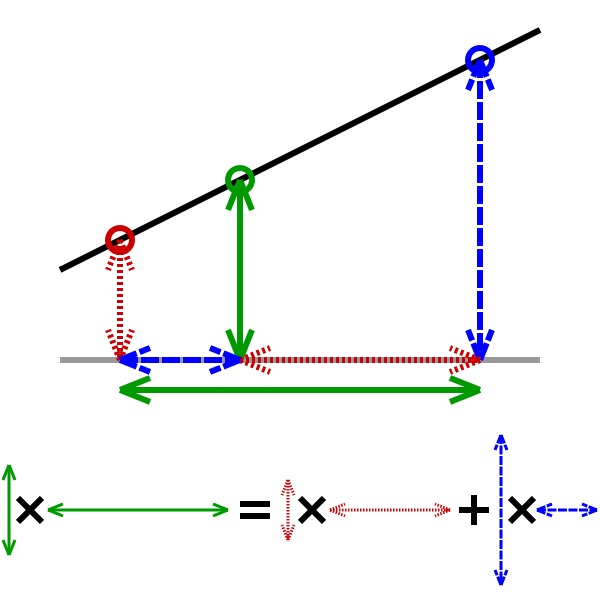
Функция glm::lerp выполняет линейную интерполяцию. Она перегружена для скаляров, для векторов из 2-4 значений и для кватернионов.
// для перегруженной glm::lerp, принимающей glm::vec3
#include <glm/gtx/compatibility.hpp>
using glm::vec2;
using glm::vec3;
using glm::vec4;
int main()
{
{
vec2 a = { 1, 3 };
vec2 b = { -3, 5 };
vec2 median = glm::lerp(a, b, 0.5f);
assert(glm::distance(median, {-1, 4}) < 0.001f);
}
{
vec3 a = { 1, 3 };
vec3 b = { -3, 5 };
vec3 median = glm::lerp(a, b, 0.5f);
assert(glm::distance(median, {-1, 4}) < 0.001f);
}
}