График двумерной функции

Все статьи / График двумерной функции

В статье рассмотрен рендеринг гладких незамкнутых поверхностей на примере графика фукнции от двух аргументов

Вспомогательный класс материала

Далее мы будем рисовать график функции новым способом, который не позволяет задать цвет вершины один раз вызовом glColor*. Это не мешает задавать цвет иным способом, но мы всё-таки прекратим использовать GL_COLOR_MATERIAL и применим функции-команды для явной установки свойств материала, который будет одинаковым для всей поверхности.

Материал в фиксированном конвейере OpenGL содержит 4 разных цвета (emission, ambient, diffuse, specular) и один параметр (shininess), влияющий размер пятна бликового (т.е. specular) компонета освещения:

Новый класс в Lights.h

class CPhongModelMaterial
{
public:
    void Setup() const;

    glm::vec4 GetEmission() const;
    glm::vec4 GetAmbient() const;
    glm::vec4 GetDiffuse() const;
    glm::vec4 GetSpecular() const;
    float GetShininess() const;

    void SetAmbient(const glm::vec4 &GetAmbient);
    void SetEmission(const glm::vec4 &GetEmission);
    void SetDiffuse(const glm::vec4 &GetDiffuse);
    void SetSpecular(const glm::vec4 &GetSpecular);
    void SetShininess(float GetShininess);

private:
    glm::vec4 m_emission;
    glm::vec4 m_ambient;
    glm::vec4 m_diffuse;
    glm::vec4 m_specular;
    float m_shininess = 10.f;
};

Реализация геттеров и сеттеров тривиальна, интересен только метод Setup, который применяет параметры материала к состоянию OpenGL:

void CPhongModelMaterial::Setup() const
{
    glMaterialfv(GL_FRONT_AND_BACK, GL_EMISSION, glm::value_ptr(m_emission));
    glMaterialfv(GL_FRONT_AND_BACK, GL_AMBIENT, glm::value_ptr(m_ambient));
    glMaterialfv(GL_FRONT_AND_BACK, GL_DIFFUSE, glm::value_ptr(m_diffuse));
    glMaterialfv(GL_FRONT_AND_BACK, GL_SPECULAR, glm::value_ptr(m_specular));
    glMaterialf(GL_FRONT_AND_BACK, GL_SHININESS, m_shininess);
}

Теперь мы добавим объект нового класса в CWindow:

class CWindow
{
    // часть определения класса пропущена
private:
    CPhongModelMaterial m_material;
};

CWindow::CWindow()
// часть конструктора пропущена
{
    m_material.SetAmbient(YELLOW_RGBA);
    m_material.SetDiffuse(YELLOW_RGBA);
    m_material.SetSpecular(FADED_WHITE_RGBA);
    m_material.SetShininess(MATERIAL_SHININESS);
}

void CWindow::OnDrawWindow(const glm::ivec2 &size)
{
    SetupView(size);
    m_sunlight.Setup();
    m_material.Setup();
    // m_surface - график двумерной функции.
    m_surface.Draw();
}

Аппроксимация графиков двумерных функций

С низкоуровневой визуализацией объектов, состоящих из плоских граней, мы познакомились. Теперь займёмся аппроксимацией (то есть приближением) криволинейных поверхностей. Поверхности будут заданы функциями от двух аргументов — y=f(x, z).

Для начала, равномерно разобьем отображаемую область функции на сетку, состоящую из SizeX*SizeZ ячеек. Затем пройдём по узлам этой сетки в цикле по X, Z и вычислим Y, который будет равен значению функции в узле сетки.

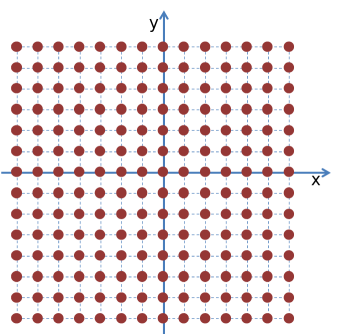
Иллюстрация

Новый класс CDottedFunctionSurface

Новый класс добавлен в файл FunctionSurface.h. Он реализует интерфейс IBody, заглушая метод Update (поверхность функции статична и не нуждается в обновлениях). Также добавлен вспомогательный синоним типа и структура данных SVertexP3N, описывающая вершину с трёхмерным вектором позиции и вектором нормали.

#pragma once

#include "IBody.h"
#include <functional>
#include <vector>
#include <glm/fwd.hpp>
#include <glm/vec3.hpp>

using Function2D = std::function<float(float, float)>;

// Вершина с трёхмерной позицией и нормалью.
struct SVertexP3N
{
    glm::vec3 position;
    glm::vec3 normal;

    SVertexP3N() = default;
    SVertexP3N(const glm::vec3 &position)
        : position(position)
    {
    }
};

class CDottedFunctionSurface final : public IBody
{
public:
    CDottedFunctionSurface(const Function2D &fn);

    /// Инициализирует сетку треугольников
    /// @param rangeX - диапазон, где x - нижняя граница, y - верхняя граница
    /// @param rangeZ - диапазон, где x - нижняя граница, y - верхняя граница
    void Tesselate(const glm::vec2 &rangeX, const glm::vec2 &rangeZ, float step);

    // IBody interface.
    void Update(float) final {}
    void Draw() const final;

private:
    Function2D m_fn;
    std::vector<SVertexP3N> m_vertices;
};

Для инициализации объекта этого класса в CWindow мы реализуем функцию GetSincFromXY, двумерный вариант тригонометрической функции sinc, также известной как кардинальный синус — то есть в итоге мы нарисуем график именно этой функции:

//////////////////////////////////////////////
// Window.h

class CWindow
{
    // часть определения класса пропущена
private:
    CSolidFunctionSurface m_surface;
};

//////////////////////////////////////////////
// Window.cpp

namespace
{
float GetSincFromXY(float x, float y)
{
    const float radius = std::hypotf(x, y);
    if (radius < std::numeric_limits<float>::epsilon())
    {
        return 1;
    }
    return sinf(radius) / radius;
}
} // anonymous namespace

CWindow::CWindow()
    : m_surface(GetSincFromXY)
// часть конструктора пропущена
{
    // график будет рисоваться в квадрате 20x20 с шагом 0,5.
    m_surface.Tesselate({-10, 10}, {-10, 10}, 0.5f);
}

void CWindow::OnDrawWindow(const glm::ivec2 &size)
{
    SetupView(size);
    m_sunlight.Setup();
    m_material.Setup();
    m_surface.Draw();
}

Заполнение массива вершин графика функции

Метод Tesselate заполняет массив несвязных вершин, используя вспомогательные функции GetPosition и CalculateNormals, а также вспомогательный конструктор структуры SVertexP3N, принимающий только позицию без нормали:

namespace
{
glm::vec3 GetPosition(const Function2D &fn, float x, float z)
{
    const float y = fn(x, z);
    return {x, y, z};
}

// вычисляет нормали численным методом,
// с помощью векторного произведения.
void CalculateNormals(std::vector<SVertexP3N> &vertices,
                      const Function2D &fn, float step)
{
    for (SVertexP3N &v : vertices)
    {
        const glm::vec3 &position = v.position;
        glm::vec3 dir1 = GetPosition(fn, position.x, position.z + step) - position;
        glm::vec3 dir2 = GetPosition(fn, position.x + step, position.z) - position;
        v.normal = glm::normalize(glm::cross(dir1, dir2));
    }
}
} // anonymous namespace

CDottedFunctionSurface::CDottedFunctionSurface(const Function2D &fn)
    : m_fn(fn)
{
}

void CDottedFunctionSurface::Tesselate(const glm::vec2 &rangeX, const glm::vec2 &rangeZ, float step)
{
    m_vertices.clear();
    // вычисляем позиции вершин.
    for (float x = rangeX.x; x < rangeX.y; x += step)
    {
        for (float z = rangeZ.x; z < rangeZ.y; z += step)
        {
            m_vertices.push_back(SVertexP3N(GetPosition(m_fn, x, z)));
        }
    }
    CalculateNormals(m_vertices, m_fn, step);
}

Применение glVertexPointer

В методе Draw мы наконец откажемся от рисования Immediate Mode (то есть от блоков glBegin/glEnd). Ранее мы отдельно задавали различные “текущие” атрибуты вершины, а функция glVertex кроме установки атрибута “позиция” ещё и порождала новую вершину.

Создатели OpenGL ещё в начале 1990-х годов поняли, что такой подход неэффективен: накладные расходы на постоянные проверки данных при каждом вызове glNormal*/glColor*/glVertex* слишком велики. Применение дисплейных списков, показанное ранее в статье “Тригонометрия и цветы”, частично решает проблему, но также имеется интерфейс для вывода целых массивов вершин несколькими вызовами функций-команд OpenGL: glVertexPointer и glDrawArrays.

У вывода целого массива вершин есть важное преимущество: такой метод работает во всех версиях и режимах OpenGL, включая

OpenGL 3.0+ в режиме Core Profile,
OpenGL ES для мобильных устройств
WebGL, реализуемый браузерами и похожий на OpenGL ES

Структура данных SVertexP3N была описана с расчётом на glVertexPointer, потому что такой метод рисования приспособлен для массивов пользовательских структур и умеет гибко адаптироваться под разные способы описания вершины. В нашем случае структура содержит вектор позиции и вектор нормали, их привязка осуществляется функциями glVertexPointer и glNormalPointer. Вместе с привязкой следует вызвать glEnableClientState, чтобы сообщить видеодрайверу, что вы планируете использовать установленный указатель на массив данных для рисования примитивов. В нашем случае вершины и нормали упакованы вместе в один массив std::vector<SVertexP3N> m_vertices, но для OpenGL это будут два разных разреженных массива:

// Включаем режим vertex array и normal array.
glEnableClientState(GL_VERTEX_ARRAY);
glEnableClientState(GL_NORMAL_ARRAY);

// Выполняем привязку vertex array и normal array
// Параметр stride задаёт число байт, прибавляемых к указателю
// для перехода к следующей вершине
// Если stride равен 0, OpenGL вычислит stride самостоятельно,
// исходя из предположения, что массив не содержит пропусков.
const size_t stride = sizeof(SVertexP3N);
// Разреженный массив нормалей получается из плотного массива вершин.
glNormalPointer(GL_FLOAT, stride, glm::value_ptr(vertices[0].normal));
// Разреженный массив позиций получается из плотного массива вершин.
glVertexPointer(3, GL_FLOAT, stride, glm::value_ptr(vertices[0].position));

// Рисуем группу примитивов, используя glDrawArrays или glDrawElements

// Выключаем режим vertex array и normal array,
// чтобы не нарушить работу legacy-кода.
glDisableClientState(GL_VERTEX_ARRAY);
glDisableClientState(GL_NORMAL_ARRAY);

Рисование с помощью glDrawArrays

Функция glDrawArrays разбирает привязанный массив вершин последовательно, разбивая их на группы по количеству вершин в примитиве. Например, при рисовании отдельных треугольников массивом из 9 вершин будет собрано 3 треугольника (по 3 вершины на каждый). При рисовании веера треугольников из 9 вершин будет собрано 7 треугольников (одна вершина станет общим центром веера, остальные сформируют его границу). Значение каждого атрибута вершины берётся из привязанного массива атрибутов.

Сейчас мы хотим нарисовать группу примитивов GL_POINT размера m_vertices.size(), начиная с 0-го элемента массива:

void CDottedFunctionSurface::Draw() const
{
    glPointSize(5.f);
    // Включаем режим vertex array и normal array.
    glEnableClientState(GL_VERTEX_ARRAY);
    glEnableClientState(GL_NORMAL_ARRAY);

    // Выполняем привязку vertex array и normal array
    const size_t stride = sizeof(SVertexP3N);
    glNormalPointer(GL_FLOAT, stride, glm::value_ptr(m_vertices[0].normal));
    glVertexPointer(3, GL_FLOAT, stride, glm::value_ptr(m_vertices[0].position));

    // Выполняем рисование массива вершин.
    glDrawArrays(GL_POINTS, 0, GLsizei(m_vertices.size()));

    // Выключаем режим vertex array и normal array.
    glDisableClientState(GL_VERTEX_ARRAY);
    glDisableClientState(GL_NORMAL_ARRAY);
}

Метод следует отрефакторить, поскольку сейчас он выполняет сразу две задачи: сначала привязывает массивы данных вершин, а затем рисует группу примитивов GL_POINT. Задачу привязки массива std::vector<SVertexP3N> m_vertices к OpenGL можно выделить в отдельную шаблонную функцию, которая в шаблонном параметре принимает ссылку на функтор, использующий привязанные массивы в своих целях. Функтором выступит лямбда-функция:

namespace
{
const float DOT_SIZE = 5.f;

/// Привязывает вершины к состоянию OpenGL,
/// затем вызывает 'callback'.
template <class T>
void DoWithBindedArrays(const std::vector<SVertexP3N> &vertices, T && callback)
{
    // Включаем режим vertex array и normal array.
    glEnableClientState(GL_VERTEX_ARRAY);
    glEnableClientState(GL_NORMAL_ARRAY);

    // Выполняем привязку vertex array и normal array
    const size_t stride = sizeof(SVertexP3N);
    glNormalPointer(GL_FLOAT, stride, glm::value_ptr(vertices[0].normal));
    glVertexPointer(3, GL_FLOAT, stride, glm::value_ptr(vertices[0].position));

    // Выполняем внешнюю функцию.
    callback();

    // Выключаем режим vertex array и normal array.
    glDisableClientState(GL_VERTEX_ARRAY);
    glDisableClientState(GL_NORMAL_ARRAY);
}
} // anonymous namespace

void CDottedFunctionSurface::Draw() const
{
    glPointSize(DOT_SIZE);
    DoWithBindedArrays(m_vertices, [this] {
        glDrawArrays(GL_POINTS, 0, GLsizei(m_vertices.size()));
    });
}

Благодаря установке размера точек равным 5 на большом расстоянии от камеры точки формируют непрерывную поверхность. Однако, вблизи камеры поверхность рассыпается:

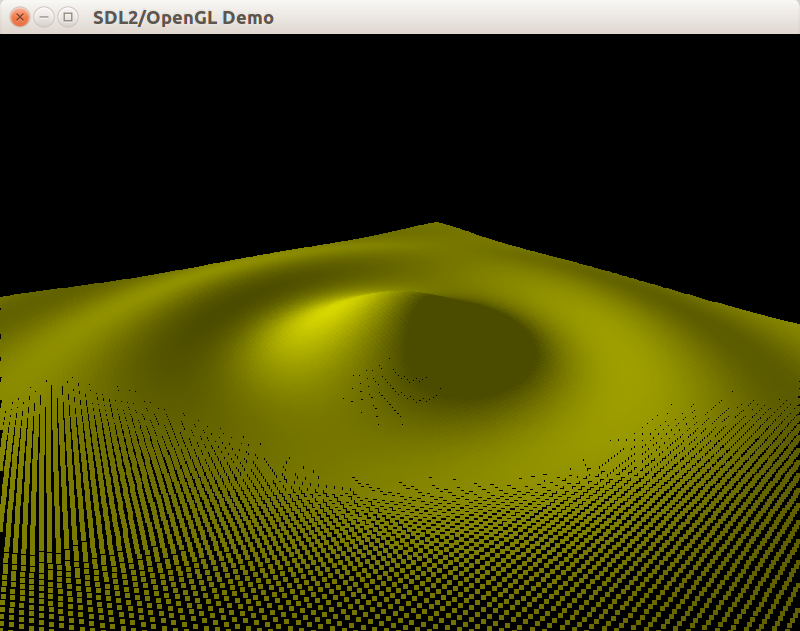
Скриншот

Замощение поверхности лентой треугольников

Теперь мы соединим вершины при помощи лент из треугольников (GL_TRIANGLE_STRIP). На первый взгляд, нам необходимо SizeY лент длиной по 2*SizeX треугольников каждая:

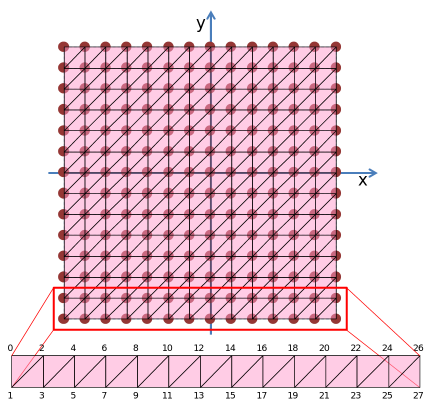
Иллюстрация

В качестве альтернативы можно было бы соединить вершины в виде набора вееров из треугольников (GL_TRIANGLE_FAN), но это потребовало бы большего количества групп примитивов:

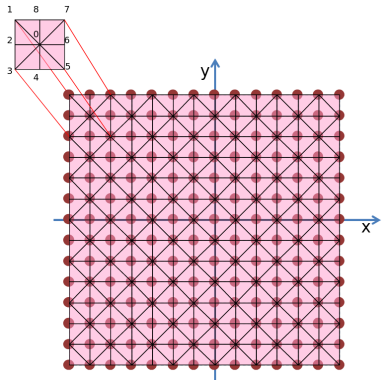
Иллюстрация

Для сокращения SizeY лент треугольников до единственной ленты мы будем «сшивать» соседние ленты треугольников, добавляя пару дополнительных вершин в конце каждой ленты — в результате вырожденный треугольник нулевой площади совершит переход к следующему ряду треугольников. Также потребуется постоянно менять направление обхода рядов ленты:

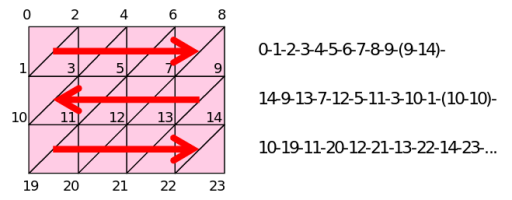
Иллюстрация

Такой прием позволит нарисовать всю сетку с помощью одной ленты из треугольников, что положительно скажется на эффективности ее обработки OpenGL.

С использованием расширения GL_NV_primitive_restart можно выполнять «перезапуск» группы примитивов и без добавления вырожденных граней и необходимости менять направление обхода рядов ленты.

Новый класс CSolidFunctionSurface

Для решения проблем с рассыпанием добавим в FunctionSurface.h новый класс CSolidFunctionSurface. Этот класс будет, подобно классам CIdentityCube и CIdentityTetrahedron, использовать опосредованный доступ к вершинам через массив, содержащий лишь индексы в массиве вершин.

class CSolidFunctionSurface final : public IBody
{
public:
    CSolidFunctionSurface(const Function2D &fn);

    /// Инициализирует индексированную сетку треугольников
    /// @param rangeX - диапазон, где x - нижняя граница, y - верхняя граница
    /// @param rangeZ - диапазон, где x - нижняя граница, y - верхняя граница
    void Tesselate(const glm::vec2 &rangeX, const glm::vec2 &rangeZ, float step);

    // IBody interface.
    void Update(float) final {}
    void Draw() const final;

private:
    Function2D m_fn;
    // содержит "палитру" вершин.
    std::vector<SVertexP3N> m_vertices;
    // содержит индексы в палитре вершин.
    std::vector<uint32_t> m_indicies;
};

Теперь функция Tesselate станет сложнее: в неё добавился код, который делит вершины по треугольникам, занося индексы в массив m_indicies. Благодаря описанному ранее трюку с переходом на новый ряд через вырожденный треугольник (с нулевой площадью) мы можем представить всю поверхность одной изогнутой сеткой треугольников:

CSolidFunctionSurface::CSolidFunctionSurface(const Function2D &fn)
    : m_fn(fn)
{
}

void CSolidFunctionSurface::Tesselate(const glm::vec2 &rangeX, const glm::vec2 &rangeZ, float step)
{
    m_vertices.clear();
    const unsigned columnCount = unsigned((rangeX.y - rangeX.x) / step);
    const unsigned rowCount = unsigned((rangeZ.y - rangeZ.x) / step);

    // вычисляем позиции вершин.
    for (unsigned ci = 0; ci < columnCount; ++ci)
    {
        const float x = rangeX.x + step * float(ci);
        for (unsigned ri = 0; ri < rowCount; ++ri)
        {
            const float z = rangeZ.x + step * float(ri);
            m_vertices.push_back(SVertexP3N(GetPosition(m_fn, x, z)));
        }
    }
    CalculateNormals(m_vertices, m_fn, step);
    // вычисляем индексы вершин.
    for (unsigned ci = 0; ci < columnCount - 1; ++ci)
    {
        if (ci % 2 == 0)
        {
            for (unsigned ri = 0; ri < rowCount; ++ri)
            {
                unsigned index = ci * rowCount + ri;
                m_indicies.push_back(index + rowCount);
                m_indicies.push_back(index);
            }
        }
        else
        {
            for (unsigned ri = rowCount - 1; ri < rowCount; --ri)
            {
                unsigned index = ci * rowCount + ri;
                m_indicies.push_back(index);
                m_indicies.push_back(index + rowCount);
            }
        }
    }
}

Рисование с помощью glDrawElements

Функция glDrawElements является альтернативой для glDrawArrays, дающей косвенный доступ к вершинам через дополнительный массив индексов — именно такой метод рисования нам и нужен. Используя ранее описанную функцию DoWithBindedArrays, выполняем рисование группы примитивов GL_TRIANGLE_STRIP:

void CSolidFunctionSurface::Draw() const
{
    DoWithBindedArrays(m_vertices, [this] {
        glDrawElements(GL_TRIANGLE_STRIP, GLsizei(m_indicies.size()),
                       GL_UNSIGNED_INT, m_indicies.data());
    });
}

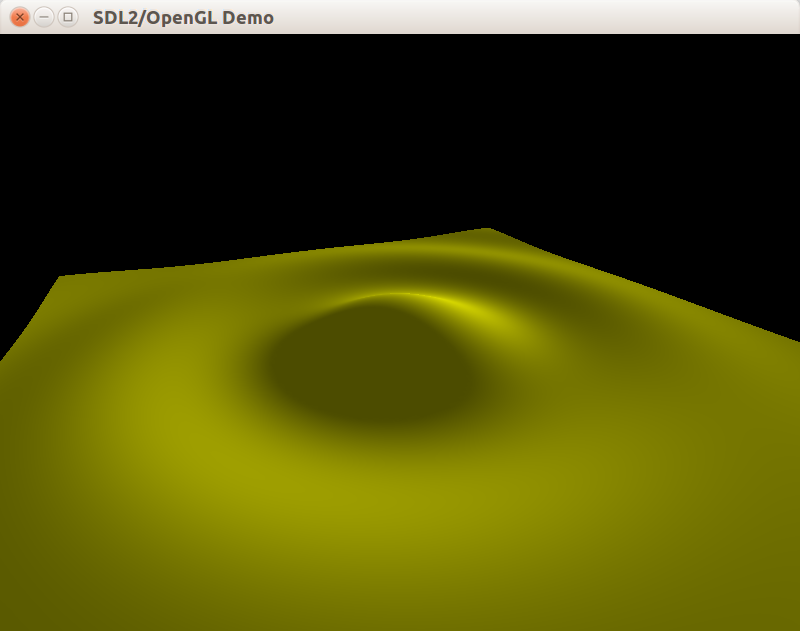
В результате мы получаем поверхность, плотно замощённую треугольниками.

Результат

Вы можете взять полный пример к уроку на github. А вот так выглядит окно после запуска:

Скриншот

Все статьи / График двумерной функции

Содержание

Вспомогательный класс материала

Новый класс в Lights.h

Аппроксимация графиков двумерных функций

Новый класс CDottedFunctionSurface

Заполнение массива вершин графика функции

Применение glVertexPointer

Рисование с помощью glDrawArrays

Замощение поверхности лентой треугольников

Новый класс CSolidFunctionSurface

Рисование с помощью glDrawElements

Результат