Тригонометрия и цветы

Все статьи / Тригонометрия и цветы

Тригонометрия и линейная алгебра незаменимы в компьютерной графике, даже если вы просто хотите нарисовать цветок. В дополнение в статье рассмотрена реализация Drag&Drop для нарисованной фигуры.

Дисплейные списки

На этот раз мы нарисуем что-нибудь более интересное, а именно вращающиеся «цветочки». Каждый цветочек будет представлен в виде искаженного круга, радиус которого – функция, зависящая от угла. Поскольку рисование круга вовлекает достаточно большое количество вычислений, воспользуемся дисплейными списками (Display Lists) - возможностью OpenGL, позволяющей сохранить последовательность вызовов функций OpenGL, а затем воспроизвести их произвольное количество раз. Такой подход может ускорить работу нашего приложения в некоторых реализациях OpenGL.

Использовать дисплейные списки очень просто. Сначала нужно сгенерировать имя для дисплейного списка (или нескольких дисплейных списков) при помощи функции glGenLists. Затем вызвать команды OpenGL между вызовами функций glNewList и glEndList. Воспроизвести записанную последовательность команд OpenGL можно при помощи функции glCallList или glCallLists.

Реализуем данный функционал внутри класса CFlower:

#pragma once

#include <glm/vec3.hpp>
#include <boost/noncopyable.hpp>

class CFlower : private boost::noncopyable
{
public:
    CFlower() = default;
    virtual ~CFlower();

    void SetupShape(float minRadius, float maxRadius, int petalCount);
    void SetCenterColor(const glm::vec3 &centerColor);
    void SetPetalColor(const glm::vec3 &petalColor);

    virtual void Draw()const;
    virtual bool HitTest(const glm::vec2 &point)const;

private:
    void DeleteList();
    void Redraw()const;
    float GetRadiusByAngle(float angle) const;

    mutable unsigned m_displayList = 0;
    float m_minRadius = 0;
    float m_maxRadius = 0;
    int m_petalCount = 0;
    glm::vec3 m_centerColor;
    glm::vec3 m_petalColor;
};

Дисплейный список — это ресурс, который нуждается в удалении. Поэтому в деструкторе мы будем проверять и очищать ресурс.

CFlower::~CFlower()
{
    if (m_displayList)
    {
        glDeleteLists(m_displayList, 1);
        m_displayList = 0;
    }
}

Метод Draw не занимается непосредственным рисованием: вместо этого он проверяет наличие дисплейного списка, заполняет его при необходимости, а затем просто выполняет список.

void CFlower::Draw() const
{
    // если дисплейный список еще не был создан, то для начала создаем его
    if (!m_displayList)
    {
        // Генерируем новый дисплейный список для цветка
        m_displayList = glGenLists(1);
        glNewList(m_displayList, GL_COMPILE);
        // Для заполнения списка вызываем redraw.
        Redraw();
        // завершаем дисплейный список
        glEndList();
    }

    // вызываем ранее созданный дисплейный список
    glCallList(m_displayList);
}

Рисуем цветок

Метод Redraw выполняет прямое рисование цветка. Отметим, что центр цветка в его локальной системе координат всегда лежит в точке (0, 0, 0). Для помещения цветка в нужное место мы в дальнейшем воспользуемся матрицей моделирования вида (но об этом чуть позже).

void CFlower::Redraw() const
{
    // угловой шаг (для рисования каждого лепестка
    // нам понадобится как минимум 20 вершин)
    const float step = float(2 * M_PI) / float(m_petalCount * 20);

    glBegin(GL_TRIANGLE_FAN);

    // центральная вершина будет иметь цвет m_centerColor
    glColor3f(m_centerColor.x, m_centerColor.y, m_centerColor.z);
    glVertex2f(0, 0);

    // вершины лепестка будут иметь цвет m_petalColor
    glColor3f(m_petalColor.x, m_petalColor.y, m_petalColor.z);
    for (float angle = 0; angle <= float(2 * M_PI) + 0.5f * step; angle += step)
    {
        // в дискретном мире компьютеров sin(2 * PI) может отличаться
        // от sin(0). Поэтому если angle подошел близко к 2*PI,
        // считаем его равным 0
        // это нужно для того, чтобы начало и конец веера
        // сошлись в одной точке
        float fixedAngle = (fabsf(angle - float(2 * M_PI)) < 1e-4f) ? 0 : angle;

        // вычисляем радиус искривленной окружности для данного угла
        float radius = GetRadiusByAngle(fixedAngle);
        float x = radius * cosf(fixedAngle);
        float y = radius * sinf(fixedAngle);

        // создаем новую вершину
        glVertex2f(x, y);
    }

    glEnd();
}

float CFlower::GetRadiusByAngle(float angle)const
{
    // вычисляем радиус искривленной окружности для данного угла.
    return 0.5f * (m_maxRadius - m_minRadius)
            * cosf(angle * m_petalCount) + m_minRadius;
}

Теперь можно создать несколько цветов:

const glm::vec3 LIGHT_YELLOW = { 1.f, 1.f, 0.5f};
const glm::vec3 RED = {1, 0, 0};
const glm::vec3 ORANGE = {1.f, 0.5f, 0.f};
const glm::vec3 YELLOW = {1.f, 1.f, 0.f};
const glm::vec4 QUIET_GREEN = {0.f, 0.5f, 0.2f, 1.f};
{
    auto pFlower = std::make_unique<CMovableFlower>();
    pFlower->SetupShape(40, 150, 6);
    pFlower->SetCenterColor(LIGHT_YELLOW);
    pFlower->SetPetalColor(RED);
    m_flowers.push_back(std::move(pFlower));
}
{
    auto pFlower = std::make_unique<CMovableFlower>();
    pFlower->SetupShape(20, 60, 5);
    pFlower->SetCenterColor(LIGHT_YELLOW);
    pFlower->SetPetalColor(ORANGE);
    m_flowers.push_back(std::move(pFlower));
}
{
    auto pFlower = std::make_unique<CMovableFlower>();
    pFlower->SetupShape(25, 70, 7);
    pFlower->SetCenterColor(RED);
    pFlower->SetPetalColor(YELLOW);
    m_flowers.push_back(std::move(pFlower));
}
SetBackgroundColor(QUIET_GREEN);

После запуска увидим такой результат:

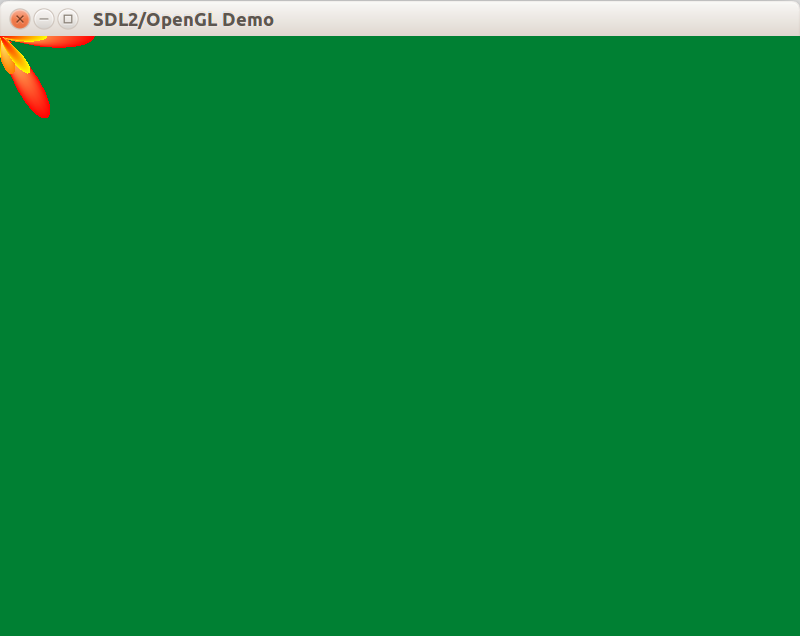
скриншот

Помещаем цветок на клумбе

Очевидно, нас не устраивает ситуация, когда все цветы сжались в левом верхнем углу экрана. Можно создать новый класс CMovableFlower, который даст цветам возможность перемещения. Линейная алгебра и OpenGL дают нам возможность реализовать перемещение, не модифицируя код класса CFlower! Таким будет объявление класса:

#pragma once

#include "Flower.h"
#include <glm/vec2.hpp>

class CMovableFlower : public CFlower
{
public:
    CMovableFlower() = default;

    void Draw()const override;
    bool HitTest(const glm::vec2 &point)const  override;

    const glm::vec2 &GetPosition()const;
    void SetPosition(const glm::vec2 &position);

private:
    glm::vec2 m_position;
};

Для этого мы воспользуемся возможностью установки матриц, которую раньше применяли для настройки проецирования изображения в кадр. Сейчас мы установим матрицу GL_MODELVIEW, при этом переключать режим матрицы с помощью glMatrixMode(GL_MODELVIEW) не надо, потому что по умолчанию этот режим уже выставлен.

Для смещения позиции цветка нам нужна трансформация перемещения (англ. translate transform) на вектор (x, y, 0). Эту матрицу мы установим как текущую, и в целях простоты проигнорируем ранее существовавшую матрицу.

void CMovableFlower::Draw() const
{
    // Модифицируем Model-View матрицу,
    // теперь она задаёт перемещение на вектор (x, y, 0)
    glm::vec3 offset = { m_position.x, m_position.y, 0.f };
    glm::mat4 transform = glm::translate(glm::mat4(), offset);
    // Сохраняем старую матрицу в стек матриц драйвера
    glPushMatrix();
    glLoadMatrixf(glm::value_ptr(transform));
    // Способ рисования не изменился
    CFlower::Draw();
    // Извлекаем старую матрицу из стека матриц драйвера
    glPopMatrix();
}

После замены CFlower на CMovableFlower, установки позиций трём цветкам и запуска программы получим:

скриншот

Drag&Drop для цветов

Садоводы вряд ли обрадуются клумбе, которую нельзя улучшить. Давайте добавим возможность перетаскивания цветов мышью, чтобы обрадовать всех садоводов страны. Вот что следует сделать:

Добавить в классы CFlower и CMovableFlower виртуальный метод HitTest, который будет производить pixel-perfect проверку пересечения точки и цветка.
Изменить функцию sdl::DispatchEvent, чтобы обработка Drag&Drop была удобнее
Добавить в CWindow обработчики событий, позволяющие реализовать захват и перетаскивание цветка.

Спецификация метода HitTest будет выглядеть примерно так:

class CFlower
{
public:
    // остальной код пропущен
    virtual bool HitTest(const glm::vec2 &point)const;
};

class CMovableFlower
{
public:
    // остальной код пропущен
    bool HitTest(const glm::vec2 &point)const override;
};

Реализовать CMovableFlower::HitTest легко:

bool CMovableFlower::HitTest(const glm::vec2 &point) const
{
    // вызываем CFlower::HitTest со смещённой проверяемой точкой.
    return CFlower::HitTest(point - m_position);
}

В случае с CFlower, точная проверка попадания точки требует применения тригонометрии. Общая идея такова: возьмём вектор от центра цветка к позиции курсора, и переведём этот вектор в полярные координаты, т.е. представим вектор как пару {угол, длина вектора}. Зная угол, мы можем вычислить переменный радиус цветка для этого угла. Зная радиус и длину вектора, мы можем просто сравнить их и точно определить, попадает ли точка в цветок. Проиллюстрируем идею:

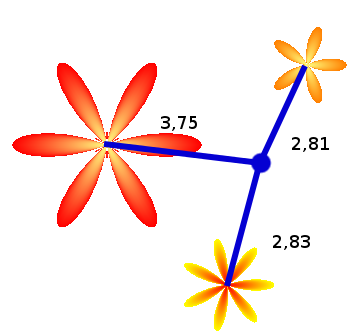
Иллюстрация

метод CFlower::HitTest

bool CFlower::HitTest(const glm::vec2 &point) const
{
    // центр всегда в точке (0, 0), так что вектор от центра
    // к point равен point; извлекаем полярный угол этого вектора.
    const float angle = std::atan2(point.y, point.x);
    const float radius = GetRadiusByAngle(angle);

    // Если длина вектора меньше радиуса, есть попадание.
    // Мы используем `glm::length` вместо point.length(), потому что
    // point.length() вернёт число компонентов вектора, т. е. число 2.
    return (glm::length(point) < radius);
}

Теперь изменим sdl::DispatchEvent, но сначала упростим интерфейс IInputEventAcceptor:

класс IInputEventAcceptor

// Принимает события SDL, разделённые по категориям.
// Деление условное и может быть изменено.
class IInputEventAcceptor
{
public:
    virtual ~IInputEventAcceptor() = default;

    virtual void OnDragBegin(const glm::vec2 &pos) { (void)pos; }
    virtual void OnDragMotion(const glm::vec2 &pos) { (void)pos; }
    virtual void OnDragEnd(const glm::vec2 &pos) { (void)pos; }
    virtual void OnKeyDown(const SDL_KeyboardEvent &) {}
    virtual void OnKeyUp(const SDL_KeyboardEvent &) {}
};

Новая диспетчеризация событий:

листинг DispatchEvent.cpp

#include "stdafx.h"
#include "DispatchEvent.h"

namespace
{
glm::vec2 GetMousePosition(const SDL_MouseButtonEvent &event)
{
    return { event.x, event.y };
}

glm::vec2 GetMousePosition(const SDL_MouseMotionEvent &event)
{
    return { event.x, event.y };
}
}

void sdl::DispatchEvent(const SDL_Event &event, IInputEventAcceptor &acceptor)
{
    switch (event.type)
    {
    case SDL_KEYDOWN:
        acceptor.OnKeyDown(event.key);
        break;
    case SDL_KEYUP:
        acceptor.OnKeyUp(event.key);
        break;
    case SDL_MOUSEBUTTONDOWN:
        acceptor.OnDragBegin(GetMousePosition(event.button));
        break;
    case SDL_MOUSEBUTTONUP:
        acceptor.OnDragEnd(GetMousePosition(event.button));
        break;
    case SDL_MOUSEMOTION:
        acceptor.OnDragMotion(GetMousePosition(event.motion));
        break;
    }
}

класс CWindow

class CWindow : public CAbstractInputControlWindow
{
public:
    CWindow();

protected:
    // CAbstractWindow interface
    void OnUpdateWindow(float deltaSeconds) override;
    void OnDrawWindow(const glm::ivec2 &size) override;

    // IInputEventAcceptor interface
    void OnDragBegin(const glm::vec2 &pos) override;
    void OnDragMotion(const glm::vec2 &pos) override;
    void OnDragEnd(const glm::vec2 &pos) override;

private:
    void SetupView(const glm::ivec2 &size);

    std::vector<std::unique_ptr<CMovableFlower>> m_flowers;
    CMovableFlower *m_draggingFlower = nullptr;
};

В методе OnDragBegin мы должны найти цветок, который задет курсором, при этом массив цветов следует обходить в порядке, обратном рисованию — иначе при наложении цветов не получится схватить тот цветок, который визуально лежит сверху:

Иллюстрация

Реализовать такой обход можно на итераторах и сырых циклах, но в современном C++ принято вместо этого использовать функциональные алгоритмы и интервалы. Воспользуемся инвертирующим адаптером boost::adaptors::reverse и алгоритмом find_if, соединённым с лямбда-функцией:

методы OnDrag*

#include <boost/range/algorithm/find_if.hpp>
#include <boost/range/adaptor/reversed.hpp>

void CWindow::OnDragBegin(const glm::vec2 &pos)
{
    auto flowers = boost::adaptors::reverse(m_flowers);
    auto it = boost::find_if(flowers, [&](const auto &pFlower) {
        return pFlower->HitTest(pos);
    });
    if (it != flowers.end())
    {
        m_draggingFlower = it->get();
    }
}

void CWindow::OnDragMotion(const glm::vec2 &pos)
{
    if (m_draggingFlower)
    {
        m_draggingFlower->MoveTo(pos);
    }
}

void CWindow::OnDragEnd(const glm::vec2 &pos)
{
    if (m_draggingFlower)
    {
        m_draggingFlower->MoveTo(pos);
        m_draggingFlower = nullptr;
    }
}

Финальные улучшения

Текущая реализация содержит один баг: при захвате цветка происходит скачок. Баг связан с тем, что мы хватаем цветок за произвольную точку, а перемещение применяем к центру, не учитывая разницу между точкой захвата и центром цвета.

Подумайте, как можно исправить этот баг с помощью нового поля glm::vec2 m_dragOffset класса CWindow.

Своё решение можете сравнить с полным примером к уроку на github.