Законы Кеплера

Все статьи / Законы Кеплера

В статье численными методами решаются уравнения Кеплера, необходимые для визуализации движения небесных тел в пределах солнечной системы.

Заголовок окна

Для удобства мы будем выводить в заголовке окна информацию о скорости симуляции солнечной системы. Для этого следует внести изменения в класс CAbstractWindow, добавив новый метод SetTitle, использующий свободную функцию SDL_SetWindowTitle для изменения заголовка окна:

// в заголовочном файле
class CAbstractWindow : private boost::noncopyable
{
public:
    // ... публичная секция не меняется

protected:
    void SetBackgroundColor(glm::vec4 const& color);
    void SetTitle(const std::string &title);
    // ... остальная часть определения класса не меняется
};

// в файле реализации

class CAbstractWindow::Impl
{
public:
    // ... начало публичной секции
    void SetBackgroundColor(const glm::vec4 &color)
    {
        m_clearColor = color;
    }

    void SetTitle(const std::string &title)
    {
        SDL_SetWindowTitle(m_pWindow.get(), title.c_str());
    }
    // ... остальная часть определения класса не меняетсяs
};

void CAbstractWindow::SetTitle(const std::string &title)
{
    m_pImpl->SetTitle(title);
}

Задача двух тел

Задача двух тел (ru.wikipedia.org) состоит в том, чтобы определить движение двух точечных частиц, которые взаимодействуют только друг с другом. Движение Луны и Земли вокруг их общего центра масс можно описать как задачу двух тел, если пренебречь гравитационным влиянием Солнца и других планет солнечной системы.

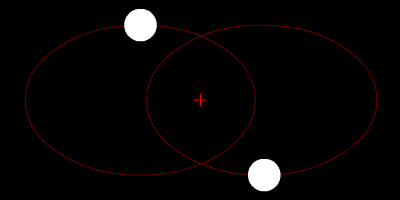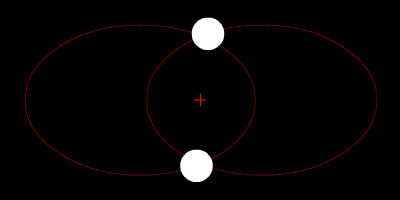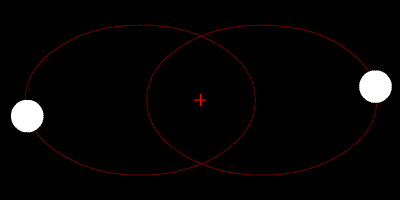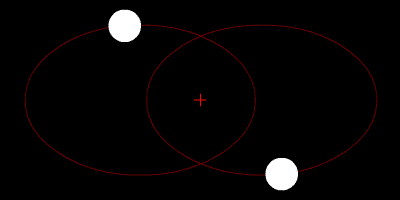
Иллюстрация

Прелесть задачи двух тел в том, что она прекрасно решается аналитически: достаточно знать зависимость силы притяжения или, например, силы кулоновского отталкивания от координат тел. Движение космических тел по эллиптической орбите в задаче двух тел описывается уравнением Кеплера (ru.wikipedia.org):

E - e * sin(E) = M

E — эксцентрическая аномалия (параметр, из которого выводится переменная величина удалённости тела от точки, вокруг которой оно вращается)
e — эксцентриситет орбиты, то есть степень отклонения эллиптической орбиты от правильной окружности
M — длина участка орбиты, пройденного с момента последнего прохождения перицентра (в солнечной системе перицентры планет называются перигелиями)

На данной иллюстрации перицентр (перигелий) орбиты тела под числом 3 обозначен числом 6, а апоцентр — числом 7:

Иллюстрация

Задача трёх (и более) тел

К сожалению, при добавлении в систему Луна-Земля влияния Солнца, а также при добавлении любого третьего тела в систему из двух тел задача нахождения координат в любой момент времени становится неразрешимой аналитическими методами. Иными словами, не существует способа с помощью решения системы уравнений точно определить траектории в системе из трёх тел.

Отсутсвие точного решения не мешает искать приближённые решения с помощью численного решения приближённых уравнений. То есть на практике задачу двух тел можно решить с любой заданной точностью — но невозможно решить абсолютно точно, за исключением некоторых частных случаев.

Движение планет по эллиптическим орбитам

В солнечной системе присутствует как минимум Солнце и 8 планет (Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун). Однако, для визуализации движения планет по их орбитам мы можем пренебречь взаимным влиянием планет и разбить Солнечную Систему на 8 подсистем “Солнце-планета”.

В каждой подсистеме “Солнце-планета” путём численного решения уравнения Кеплера можно определить зависимость координат планеты от времени. Для этих целей создадим вспомогательный класс CEllipticOrbit:

#pragma once

#include <glm/mat4x4.hpp>
#include <glm/vec2.hpp>
#include <cmath>

class CEllipticOrbit
{
public:
    CEllipticOrbit(
        double const& largeAxis,     // большая полуось эллипса
        double const& eccentricity,  // эксцентриситет орбиты
        double const& meanMotion,    // среднее движение (градуcов за единицу времени)
        double const& periapsisEpoch // начальная эпоха прохождения через перигелий
        ):
    m_largeAxis(largeAxis),
    m_eccentricity(eccentricity),
    m_meanMotion(meanMotion),
    m_periapsisEpoch(periapsisEpoch)
    {
    }

    double Eccentricity()const;
    double LargeAxis()const;

    glm::vec2 PlanetPosition2D(double const& time)const;

private:
    double MeanAnomaly(const double &time)const;
    double EccentricityAnomaly(const double &time)const;
    double TrueAnomaly(const double &eccentricityAnomaly)const;
    double RadiusVectorLength(const double &eccentricityAnomaly)const;

    double m_largeAxis;
    double m_eccentricity;
    double m_meanMotion;
    double m_periapsisEpoch;
};

Численное решение уравнения Кеплера

Численные методы поиска корней уравнений позволяют найти решения уравнения с заданной степенью точности. Если вспомнить, что числа в памяти компьютера сами по себе ограничены в точности представления, то несложно сделать вывод, что в дискретном мире компьютеров численное решение по своей точности мало чем отличается от аналитического. Какая разница, как вы находите √2, если √2 невозможно точно представить как float или double?

Именно поэтому мы воспольуемся численным алгоритмом поиска корней под названием метод Халли. Для сокращения кода воспользуемся готовой реализацией этого алгоритма в функции boost::math::tools::halley_iterate.

Для запуска этой функции мы должны сформировать функтор, который будет для заданного параметра x возвращать кортеж из трёх значений:

значение функции для аргумента x
значение первой производной этой функции для аргумента x
значение второй производной этой функции для аргумента x

В C++98 нам бы пришлось писать новый класс с перегруженным оператором вызова, но в C++11 мы можем применить лямбда-функции:

// Матчасть взята отсюда: http://www.astronet.ru/db/msg/1190817/node21.html#ll60

// Уравнение кеплера, задающее связь между эксцентрической аномалией,
// эксцентриситетом орбиты и средней аномалией
//      M = E - e * sin(E)
// где M - средняя аномалия, e - эксцентриситет орбиты, E - эксцентрическая аномалия
// уравнение `M = E - e * sin(E)` преобразуется так, чтобы слева было число 0,
// а справа - некоторая функция F(E):
//      0 = E - M - e * sin(E)
// Функтор возвращает функцию от E, а также две её производные функции.
//      F(E) = E - M - e * sin(E)
//      F'(E) = 1 - e * cos(E)
//      F''(E) = e * sin(E)
using FunctionSnapshot = boost::math::tuple<double, double, double>;
using EquationFunction = std::function<FunctionSnapshot(const double &x)>;

EquationFunction MakeKeplerEquationFunction(double meanAnomaly, double eccentricity)
{
    return [=](const double &x) {
        return boost::math::make_tuple(
                    // функция
                    x - meanAnomaly - eccentricity * sin(x),
                    // её первая производная
                    1 - eccentricity * cos(x),
                    // её вторая производная
                    eccentricity * sin(x));
    };
}

Теперь можно написать функцию-обёртку, использующую функтор с алгоритмом “метод Халли”:

// Функция выполняет численое решение уравнения кеплера,
// вычисляя эксцентрическую аномалию
// при известных средней аномалии и эксцентриситете орбиты
// В качестве решения используется метод Halley
// (http://en.wikipedia.org/wiki/Halley's_method),
// используя соответствующие алгоритмы библиотеки boost.
double SolveKeplerEquation(double const& meanAnomaly, double const& eccentricity)
{
    const int digits = (std::numeric_limits<double>::digits) >> 1;
    // ограничиваем максимальное число итераций,
    // поскольку мы рисуем систему планет в реальном времени.
    boost::uintmax_t maxIteractions = 1000;

    return boost::math::tools::halley_iterate(
        MakeKeplerEquationFunction(meanAnomaly, eccentricity),
        meanAnomaly,                // первое приближение корня
        meanAnomaly - eccentricity, // минимальное значение корня
        meanAnomaly + eccentricity, // максимальное значение корня
        digits,                     // число разрядов
        maxIteractions);            // наибольшее число итераций
}

Теперь, обладая способом решения уравнения Кеплера для заданного момента времени, мы можем реализовать остальные методы. Кроме того, мы добавим релизацию геттеров свойств:

double CEllipticOrbit::Eccentricity() const
{
    return m_eccentricity;
}

double CEllipticOrbit::LargeAxis() const
{
    return m_largeAxis;
}

double CEllipticOrbit::MeanAnomaly(const double &time) const
{
    const double anomaly = 2 * M_PI * m_meanMotion * (time - m_periapsisEpoch);
    const double wrappedAnomaly = fmod(anomaly, M_PI + M_PI);
    return wrappedAnomaly;
}

double CEllipticOrbit::EccentricityAnomaly(const double &time) const
{
    return SolveKeplerEquation(MeanAnomaly(time), m_eccentricity);
}

double CEllipticOrbit::TrueAnomaly(const double &eccentricityAnomaly) const
{
    // Тангенс половинчатого угла
    const double tg_v_2 = sqrt((1 + m_eccentricity) / (1 - m_eccentricity)) * tan(eccentricityAnomaly / 2);
    // Половинчатый угол
    const double v_2 = atan(tg_v_2);
    // Истинная аномалия
    return v_2 + v_2;
}

double CEllipticOrbit::RadiusVectorLength(const double &eccentricityAnomaly) const
{
    return m_largeAxis * (1 - m_eccentricity * cos(eccentricityAnomaly));
}

glm::vec2 CEllipticOrbit::PlanetPosition2D(const double &time) const
{
    const double e = EccentricityAnomaly(time);
    const float r = float(RadiusVectorLength(e));
    const float v = float(TrueAnomaly(e));
    return { r * cosf(v), r * sinf(v) };
}

Реализуем класс CSolarSystem

Теперь мы добавим класс, инкапсулирующий в себе информацию о Солнце, планетах и взаимодействии между ними. В целом он будет похож на класс CParticleSystem, хотя законы движения кардинально изменились: больше нет никакой случайности и хаотичности, на смену им пришли законы небесной механики.

Так выглядит объявление CSolarSystem:

#pragma once

#include "EllipticOrbit.h"
#include <glm/vec3.hpp>

class CSolarSystem
{
public:
    CSolarSystem();

    void Update(float deltaTime);
    void Draw();

    float GetViewScale()const;
    float GetTimeSpeed()const;
    unsigned GetYear()const;
    void ZoomIn();
    void ZoomOut();
    void SpeedupTime();
    void SlowdownTime();

private:
    void DrawSun();
    void DrawOrbit(const CEllipticOrbit &orbit);
    void DrawPlanets();

    float m_time;
    float m_timeSpeed;
    float m_viewScale;

    struct PlanetInfo
    {
        CEllipticOrbit orbit;
        glm::vec3 color;
        float size;
    };
    std::vector<PlanetInfo> m_planets;
};

В конструкторе CSolarSystem зададим все 8 планет, планетоид Плутон и комету Галлея:

namespace
{
const float DEFAULT_TIME_SPEED = 0.1f;
// 40 пикселей на астрономическую единицу
const float DEFAULT_SCALE = 100.f;

double GetRadians(double degrees, double seconds = 0)
{
    return glm::radians(degrees + seconds / 60.0);
}

glm::vec3 FromRGB(unsigned colorCode)
{
    unsigned r = (colorCode >> 16) % 256;
    unsigned g = (colorCode >> 8) % 256;
    unsigned b = colorCode % 256;

    return { float(r) / 255.f, float(g) / 255.f, float(b) / 255.f };
}

const glm::vec3 MERCURY_COLOR = FromRGB(0x5B71FF);
const glm::vec3 VENUS_COLOR = FromRGB(0xFFDB59);
const glm::vec3 EARTH_COLOR = FromRGB(0x168EFF);
const glm::vec3 MARS_COLOR = FromRGB(0xFF7A68);
const glm::vec3 JUPITER_COLOR = FromRGB(0x897AFF);
const glm::vec3 SATURN_COLOR = FromRGB(0x47FF81);
const glm::vec3 URANUS_COLOR = FromRGB(0xFFF463);
const glm::vec3 NEPTUNE_COLOR = FromRGB(0xFFF463);
const glm::vec3 PLUTO_COLOR = FromRGB(0xFFF463);
const glm::vec3 COMET_COLOR = FromRGB(0xFFFFFF);
}

CSolarSystem::CSolarSystem()
    : m_time(0)
    , m_timeSpeed(DEFAULT_TIME_SPEED)
    , m_viewScale(DEFAULT_SCALE)
{
    m_planets =
    {
        {CEllipticOrbit(0.387, 0.206, 1 / 0.241, GetRadians(7, 0)), MERCURY_COLOR, 1},
        {CEllipticOrbit(0.723, 0.007, 1 / 0.635, GetRadians(3, 24)), VENUS_COLOR, 3},
        {CEllipticOrbit(1.000, 0.017, 1 / 1.000, GetRadians(0)), EARTH_COLOR, 3},
        {CEllipticOrbit(1.524, 0.093, 1 / 1.881, GetRadians(1, 1)), MARS_COLOR, 2},
        {CEllipticOrbit(5.203, 0.048, 1 / 11.862, GetRadians(1, 18)), JUPITER_COLOR, 6},
        {CEllipticOrbit(6.539, 0.056, 1 / 20.658, GetRadians(2, 29)), SATURN_COLOR, 5},
        {CEllipticOrbit(19.190, 0.048, 1 / 84.800, GetRadians(0, 45)), URANUS_COLOR, 5},
        {CEllipticOrbit(30.081, 0.009, 1 / 154.232, GetRadians(1, 47)), NEPTUNE_COLOR, 5},
        {CEllipticOrbit(38.525, 0.249, 1 / 247.305, GetRadians(17, 9)), PLUTO_COLOR, 1},
        {CEllipticOrbit(17.800, 0.967, 1 / 75.300, GetRadians(162, 3)), COMET_COLOR, 0.5},
    };

}

Теперь добавим реализации Update и Draw. Планеты и Солнце мы будем рисовать как точки фиксированного размера, а орбиты — с помощью пунктирной линии. В любом случае, параметры эллипса орбиты и позицию планеты в заданный момент времени можно узнать у помощью объекта класса CElipticOrbit:

void CSolarSystem::Update(float deltaTime)
{
    m_time += deltaTime * m_timeSpeed;
}

void CSolarSystem::Draw()
{
    DrawSun();
    DrawPlanets();
}

void CSolarSystem::DrawSun()
{
    glPointSize(2.f * sqrtf(m_viewScale));
    glBegin(GL_POINTS);
    {
        glColor3f(1, 1, 0);
        glVertex2d(0, 0);
    }
    glEnd();
}

void CSolarSystem::DrawOrbit(const CEllipticOrbit &orbit)
{
    glDisable(GL_POINT_SMOOTH);
    glPointSize(1);
    glColor3f(0.5, 0.5, 0.5);
    glBegin(GL_POINTS);
    {
        // const float period = 2 * M_PI / orbit.MeanMotion();
        const float a = float(orbit.LargeAxis());
        const float e = float(orbit.Eccentricity());
        const float step = float(2 * M_PI) / (a * m_viewScale);
        const float c = e * a;
        const float k = sqrtf(1.f - e * e);
        const float b = k * a;
        const float centerX = -c;
        const float centerY = 0;

        float time = 0;
        while (time < float(2 * M_PI))
        {
            glVertex2f(centerX + a * cosf(time), centerY + b * sinf(time));
            time += step;
        }
    }
    glEnd();
}

void CSolarSystem::DrawPlanets()
{
    for (PlanetInfo const& planet : m_planets)
    {
        DrawOrbit(planet.orbit);

        glColor3fv(glm::value_ptr(planet.color));

        glEnable(GL_POINT_SMOOTH);
        glPointSize(planet.size * sqrtf(m_viewScale) / 4.f);
        glBegin(GL_POINTS);
        {
            glm::vec2 pos = planet.orbit.PlanetPosition2D(double(m_time));
            glVertex2f(pos.x, pos.y);
        }
        glEnd();
    }
}

Методы для запроса свойств и управляющие методы для изменения масштаба и скорости течения времени можно реализовать так:

namespace
{
const float MIN_TIME_SPEED = -20;
const float MAX_TIME_SPEED = +20;
const float TIME_ADJUSTMENT = 0.02f;
const float MIN_SCALE = 5;
const float MAX_SCALE = 500;
const float SCALE_FACTOR = 1.f;
}

float CSolarSystem::GetViewScale() const
{
    return m_viewScale;
}

float CSolarSystem::GetTimeSpeed() const
{
    return m_timeSpeed;
}

unsigned CSolarSystem::GetYear() const
{
    return unsigned(m_time) + INITIAL_YEAR;
}

void CSolarSystem::ZoomIn()
{
    m_viewScale *= SCALE_FACTOR;
    if (m_viewScale > MAX_SCALE)
    {
        m_viewScale = MAX_SCALE;
    }
}

void CSolarSystem::ZoomOut()
{
    m_viewScale /= SCALE_FACTOR;
    if (m_viewScale < MIN_SCALE)
    {
        m_viewScale = MIN_SCALE;
    }
}

void CSolarSystem::SpeedupTime()
{
    m_timeSpeed = m_timeSpeed + TIME_ADJUSTMENT;
    if (m_timeSpeed > MAX_TIME_SPEED)
    {
        m_timeSpeed = MAX_TIME_SPEED;
    }

    m_timeSpeed = floorf(m_timeSpeed * 1000.f + 0.5f) / 1000.f;
}

void CSolarSystem::SlowdownTime()
{
    m_timeSpeed = m_timeSpeed - TIME_ADJUSTMENT;
    if (m_timeSpeed < MIN_TIME_SPEED)
    {
        m_timeSpeed = MIN_TIME_SPEED;
    }
    m_timeSpeed = floorf(m_timeSpeed * 1000.f + 0.5f) / 1000.f;
}

Реализуем класс CWindow

Практически все возможности программы уже реализованы, в CWindow остаётся лишь управляющий код. Поэтому объявление класса CWindow будет кратким:

#pragma once
#include "DispatchEvent.h"
#include "SolarSystem.h"
#include <vector>

class CWindow : public CAbstractInputControlWindow
{
public:
    CWindow();

protected:
    // CAbstractWindow interface
    void OnUpdateWindow(float deltaSeconds) override;
    void OnDrawWindow(const glm::ivec2 &size) override;
    // IInputEventAcceptor interface
    void OnKeyDown(const SDL_KeyboardEvent &) override;

private:
    void SetupView();

    CSolarSystem m_system;
    glm::ivec2 m_windowSize;
};

В первую очередь рассмотрим реализацию конструктора, обновления состояния и рисования сцены:

namespace
{
const glm::vec4 BLACK = {0, 0, 0, 1};
}

CWindow::CWindow()
{
    SetBackgroundColor(BLACK);
    glEnable(GL_POINT_SMOOTH);
    glHint(GL_POINT_SMOOTH_HINT, GL_NICEST);
}

void CWindow::OnUpdateWindow(float deltaSeconds)
{
    m_system.Update(deltaSeconds);

    // обновляем заголовок окна
    char timeString[20];
    sprintf(timeString, "%.2f", double(m_system.GetTimeSpeed()));
    SetTitle("Year " + std::to_string(m_system.GetYear())
             + " (" + std::string(timeString) + " years/second)");
}

void CWindow::OnDrawWindow(const glm::ivec2 &size)
{
    m_windowSize = size;
    SetupView();
    m_system.Draw();
}

Метод SetupView подвергся модификациям: теперь матрица ортографического проецирования должна учитывать масштаб Солнечной Системы:

void CWindow::SetupView()
{
    const float viewScale = m_system.GetViewScale();
    // Матрица ортографического проецирования изображения в трёхмерном пространстве
    // из параллелепипеда с размером, равным (size.X x size.Y x 2).
    const float halfWidth = float(m_windowSize.x) * 0.5f / viewScale;
    const float halfHeight = float(m_windowSize.y) * 0.5f / viewScale;
    const glm::mat4 matrix = glm::ortho<float>(-halfWidth, halfWidth, -halfHeight, halfHeight);
    glViewport(0, 0, m_windowSize.x, m_windowSize.y);
    glMatrixMode(GL_PROJECTION);
    glLoadMatrixf(glm::value_ptr(matrix));
    glMatrixMode(GL_MODELVIEW);
}

Управляющие клавиши

Последним штрихом добавим в CWindow::OnKeyDown обработку управляющих клавиш. Список горячих клавиш:

клавиша “+” (точнее, клавиша “=”) увеличивает масштаб
клавиша “-“ уменьшает масштаб
клавиша “влево” уменьшает скорость течения времени, и может даже обратить время вспять
клавиша “вправо” увеличивает скорость течения времени

Поскольку вся необходимая работа уже проделана в классе CSolarSystem, в методе OnKeyDown мы просто отображаем события на методы:

void CWindow::OnKeyDown(const SDL_KeyboardEvent &event)
{
    switch (event.keysym.sym)
    {
    case SDLK_LEFT:
        m_system.SlowdownTime();
        break;
    case SDLK_RIGHT:
        m_system.SpeedupTime();
        break;
    case SDLK_EQUALS:
        m_system.ZoomIn();
        SetupView();
        break;
    case SDLK_MINUS:
        m_system.ZoomOut();
        SetupView();
        break;
    }
}

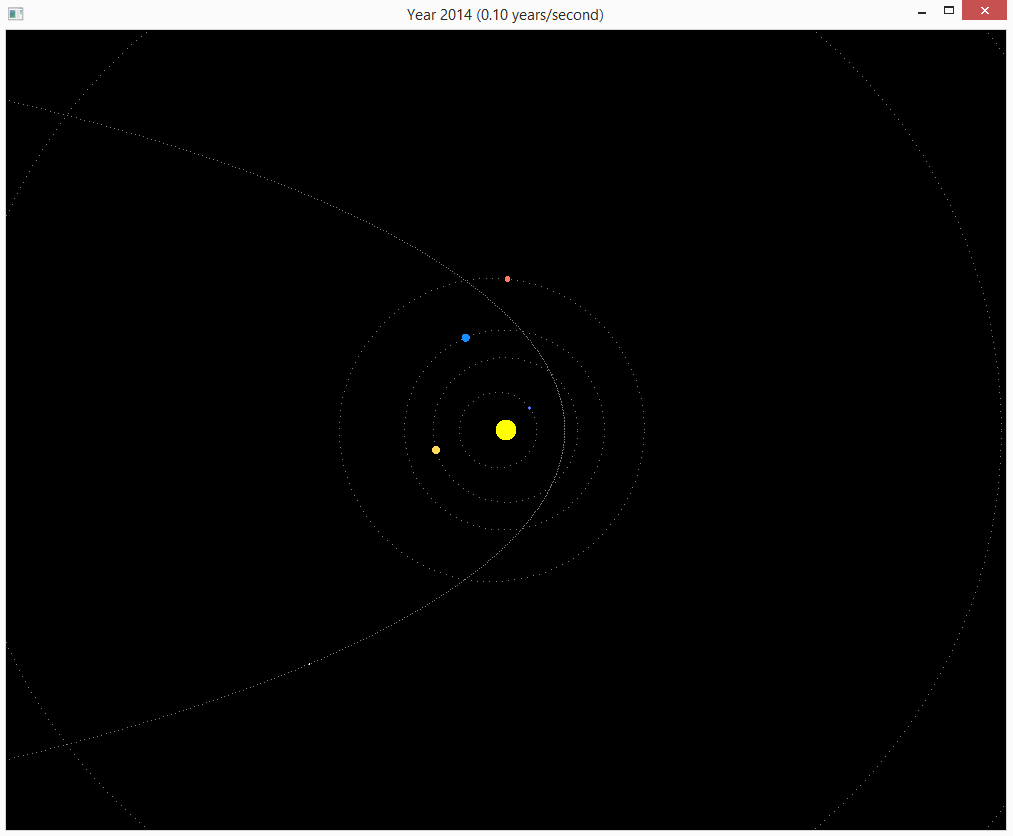
Финальная версия

Полный пример к статье доступен на github. Вот так выглядит окно после запуска:

Иллюстрация

Все статьи / Законы Кеплера

Содержание

Заголовок окна

Задача двух тел

Задача трёх (и более) тел

Движение планет по эллиптическим орбитам

Численное решение уравнения Кеплера

Реализуем класс CSolarSystem

Реализуем класс CWindow

Управляющие клавиши

Финальная версия