Все статьи Массовые столкновения
На этом занятии вы научитесь программировать игры уровня Бильярда или Arkanoid
Выполните задания, соблюдая стиль кодирования. Готовые задания должны быть выложены на github.
Задание workshop2.1
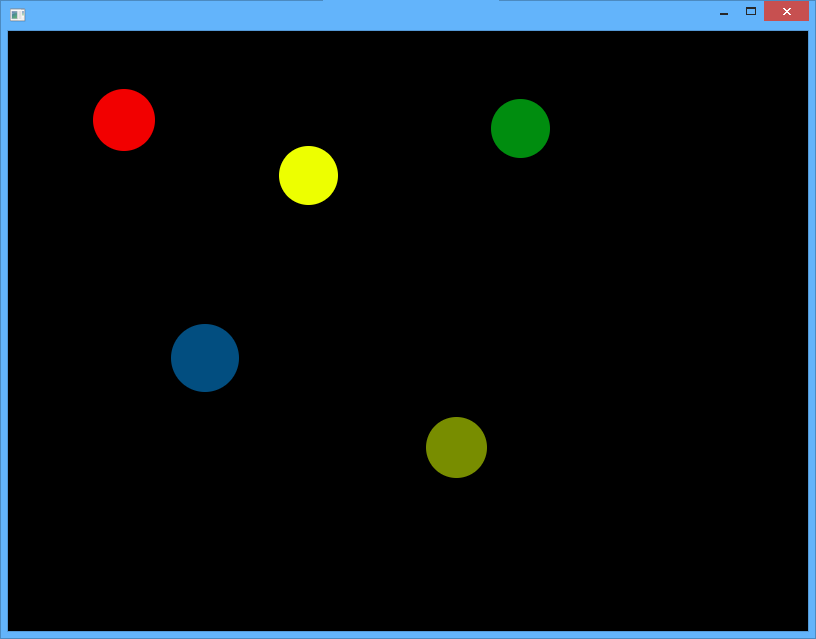
Напишите программу, в которой несколько разноцветных шаров летают в пределах окна, отталкиваясь от стенок
- шарам не нужно сталкиваться между собой
- цвета и начальные скорости шаров задаются прямо в коде без какого-либо механизма случайностей
- для выполнения задания вы можете использовать массив либо
std::vector - скорость и CircleShape шара лучше поместить в структуру, и использовать массив структур
Перед выполнением задачи изучите статью Массивы в C++. Вы можете использовать инициализацию массива при объявлении, чтобы сделать код более аккуратным и читаемым.
Задание workshop2.2 (до 2 баллов)
Добавьте шарам возможность отталкиваться друг от друга.
Для обнаружения столкновений достаточно сравнить все возможные пары шаров: если расстояние между центрами меньше суммы радиусов, шары сталкиваются. Перебрать каждую пару объектов ровно один раз можно с помощью вложенного цикла:
constexpr size_t SIZE = 100;
Ball balls[SIZE];
// Перебираем каждую пару объектов
// - ни одну пару не используем дважды
// - не используем пары из одного объекта (т.е. объект не сталкивается сам с собой)
for (size_t fi = 0; fi < SIZE; ++fi)
{
for (size_t si = fi + 1; si < SIZE; ++si)
{
// проверяем столкновение fi, si
}
}
Такой цикл среди всех возможных сочетаний элементов переберёт только пары разных элементов, и ни одну пару не переберёт дважды:
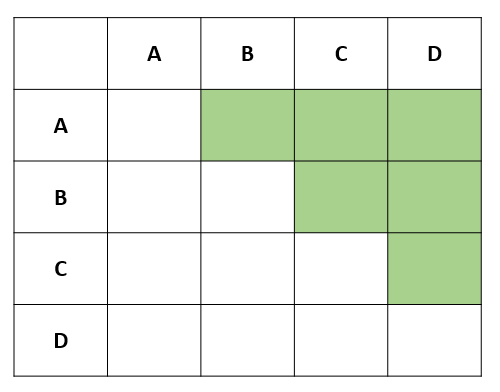
При расчёте скоростей после удара важны скорости шаров до удара и взаимное положение их центров (при условии, что массы шаров равны). Это проиллюстрировано рисунке:

Считайте, что шары имеют одинаковую массу, а столкновение абсолютно упругое. В этом случае скорости шаров после удара вычисляются так, как показано на схеме:

Как понять, что всё работает правильно
Достаточно проверить соблюдение основных закономерностей. Для удобства вы можете снять видеозапись экрана и оценивать работу столкновений на ней.
- Закон сохранения импульса в векторной форме должен сохраняться
- проверьте, что суммарный вектор скорости до столкновения равен (с погрешностью 0.01) суммарному вектору скоростей после столкновения
- Суммарная кинетическая энергия шаров в системе должна оставаться неизменной; если скорости шариков нарастают или падают, значит, вы делаете что-то неправильно.
Задание workshop2.3
Перед выполнением задачи изучите статью Генерация случайных чисел в Modern C++.
Добавьте случайную генерацию скоростей для шаров. Скорости не должны быть слишком большими или слишком маленькими: при генерации случайных чисел надо задать разумные ограничения.
Задание workshop2.4 (дополнительное, до 2 баллов)
Изучите документацию класса sf::Color.
Затем добавьте случайную генерацию цвета шаров. Выбирать случайный цвет можно, например, следующим методом:
- Создать массив предопределённых значений типа sf::Color (достаточно 8 цветов на ваш вкус), этот массив будет служить палитрой
- Реализовать случайную генерацию индекса в этом массиве
- Получив случайный индекс, запросить из палитры цвет с этим индексом
Составить хорошую палитру поможет сайт websafecolors.info.
Задание оценивается вполовину, если вы лишь берёте цвет из палитры. Для получения полных баллов надо повысить случайность цвета:
- выбирать два случайных индекса вместо одного
- полученные из палитры два цвета комбинировать путём вычисления среднего арифметического их RGBA-значений
Задание workshop2.5 (дополнительное, до 2 баллов)
Добавьте возможность создавать шар со случайным цветом и скоростью по клику левой кнопкой мыши.
- шар не должен создаваться, если после создания он бы сразу пересёкся с другим шаром (другими словами, нельзя создать шар над другим шаром)
- для хранения динамического массива шаров вам не подойдёт массив в стиле
Ball balls[...], используйтеstd::vector
Задание workshop2.6 (дополнительное, до 2 баллов)
Добавьте шарикам время жизни: каждый шар после создания существует ровно 10 секунд, после чего исчезает.
- счётчик оставшегося времени жизни лучше держать в структуре Ball
- удаление отживших своё элементов массива шаров можно выполнять с помощью идиомы
remove_if + erase; изучите, как эта идиома реализуется в C++, и используйте её - удаление отживших своё элементов удобнее выделить в функцию removeDeathBalls, обновление времени жизни всех шаров удобно выделить в функцию updateBallLifetimes
Если вы допускаете существенные ошибки в реализации remove_if + erase, то задание оценивается вполовину.
Хорошая статья: C++ std::remove_if with lambda explained
Задание workshop2.7 (дополнительное)
Могут возникать ситуации, когда шарики под воздействием других шариков “заталкиваются” друг в друга:

Решить эту проблему можно, если в процедуре update интервал каждого кадра разделить на 5-10 небольших интервалов, и на каждом из этих маленьких интервалов выполнять полный расчёт физики. Уменьшение временных интервалов при расчётах физики уменьшит вероятность заталкивания, т.к. за один интервал шарики будут передвигаться на меньшее расстояние.
При таком решении производительность не пострадает: если у вас меньше 1000-10000 шариков, то рисование шариков всё равно будет занимать больше ресурсов процессора, чем расчёт физики. Только на большом числе шариков квадратичная сложность попарного перебора окажет заметное влияние.
Задание workshop2.8 (дополнительное)
Освоить работу с макросом assert вам поможет статья Assert. Что это?.
С помощью инструкции assert добавьте проверку соблюдения законов сохранения энергии и импульса при проверке столкновений:
- закон сохранения энергии (уравнение умножено на 2):
m1 * v1^2 + m2 * v2^2 = m1 * w1^2 + m2 * w2^2- v1, v2 - скорости до столкновения
- w1, w2 - скорости после столкновения
- m1, m2 - массы шариков
- закон сохранения импульса:
m1 * v1 + m2 * v2 = m1 * w1 + m2 * w2 - можно считать, что все массы равны константе либо вычисляются как произведение константы и
R^3, где R - радиус шара
Проверка через assert должна выполняться после расчёта отталкивания очередной пары шариков.
Сравнивать числа с плавающей точкой через == не стоит: при вычислениях возможны погрешности, из-за которых ожидаемое и реальное значение будут равны лишь приблизительно. Для сравнения лучше проверить, что разница между числами не превышает 0.01:
#include <cmath>
bool areFuzzyEqual(float a, float b)
{
constexpr float tolerance = 0.01f;
const bool areEqual = (std::abs(a - b) < tolerance);
return areEqual;
}
Однако, при проверке закона сохранения энергии может возникнуть проблема: если скорости будут достаточно велики, то разница между квадратами скоростей может превысить 0.01. В этом случае разумно проверять относительную погрешность, а не абсолютную. С другой стороны, для чисел вблизи нуля относительная погрешность может быть большой даже в нормальной ситуации. Например, относительная погрешность между 0.00001 и 0 бесконечно велика. Поэтому лучше всего комбинировать расчёт относительной и абсолютной погрешностей.
Мы можем доработать функцию areFuzzyEqual, чтобы выбирать между относительной и абсолютной погрешностями в зависимости от величины чисел:
#include <cmath>
// Сравнение с допустимой абсолютной погрешностью
bool areCloseAbsolute(float a, float b, float tolerance = 0.001f)
{
return std::abs(a - b) < tolerance;
}
// Сравнение с допустимой относительной погрешностью
bool areCloseRelative(float a, float b, float tolerance = 0.001f)
{
return std::abs((a - b) / b) < tolerance;
}
// Сравнение двух чисел с плавающей точкой с допустимой погрешностью 0.001
bool areFuzzyEqual(float a, float b)
{
constexpr float tolerance = 0.001f;
if (std::abs(b) > 1.f)
{
return areCloseRelative(a, b, tolerance);
}
return areCloseAbsolute(a, b, tolerance);
}